დღეს, 14 მარტს, მსოფლიოში რიცხვ პის დღე აღინიშნება. მიზეზი მარტივია — მესამე თვის რიცხვი 14.

π-ს შესახებ ალბათ გსმენიათ და ისიც იცით, რომ წრეწირის სიგრძის მის დიამეტრთან შეფარდების ტოლია. ყველამ, ვინც სკოლაში ოდნავ ყურადღებას მაინც უთმობდა გაკვეთილებს იცის, რომ მისი მნიშვნელობა 3,14-ს უდრის; შედარებით ცოტას ახსოვს, რომ უფრო ზუსტად იგი 3,14159-ია; ხოლო დანარჩენებს, ყურმოკრული მაინც აქვთ, რომ სინამდვილეში, ეს რიცხვი საერთოდ არ მთავრდება და უსასრულო რაოდენობის ციფრებისგან შედგება.

წარმოგიდგენთ 3 GIF-ს, რომელიც ყველაზე მარტივად აგიხსნით, რა არის და საიდან მოდის პი.

GIF #1

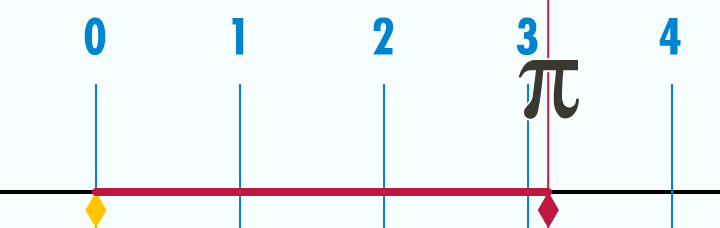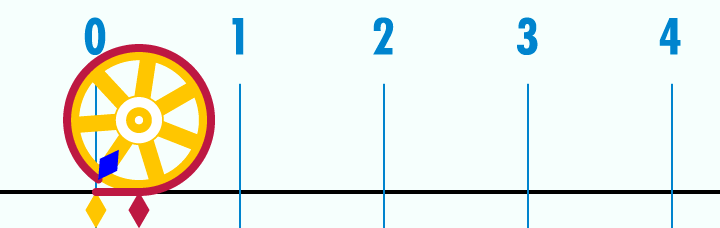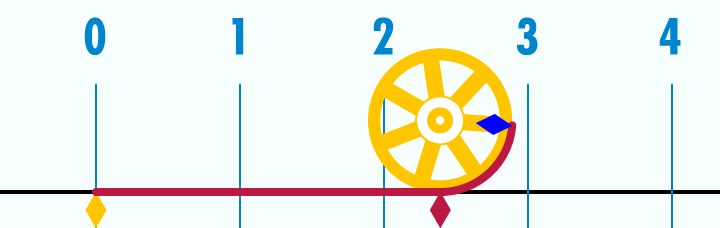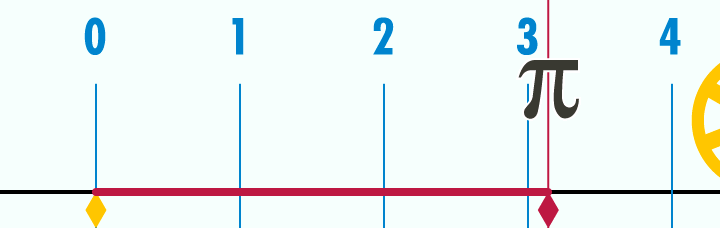
ფოტო: Wikipedia

რადგან π წრეწირის სიგრძის და დიამეტრის შეფარდებაა, თუკი ავიღებთ ერთეულოვან წრეწირს (ანუ წრეწირს, რომლის დიამეტრი 1 პირობითი ერთეულის ტოლია) და გავშლით მას წრფეზე, ერთეული სიგრძის დიამეტრი ამ მონაკვეთში 3-ზე ცოტა მეტჯერ უნდა ჩაეტიოს. უფრო ზუსტად კი — 3,14-ჯერ. კიდევ უფრო ზუსტად კი... 3,14159-ჯერ. საბოლოო სიზუსტით ამ რიცხვს ვერასდროს დავწერთ, რადგან, როგორც უკვე აღვნიშნეთ, ის არასოდეს მთავრდება.

GIF #2

ფოტო: Nerdist

მეორე გზა, რომლითაც π-ს გააზრება შეგვიძლია, კუთხის საზომი ერთეული — რადიანია. ერთი რადიანი არის წრის ორ რადიუსს შორის არსებული კუთხე, რომლის შესაბამისი რკალის სიგრძეც, თავად ამ რადიუსების ტოლია. თუკი გავზომავთ, ვნახავთ, რომ ნახევარ წრეში 3 ცალი რადიანი და კიდევ სულ ცოტა (0,14159…) ეტევა. დაკვირვებულები უკვე შეამჩნევდით, რომ ეს რიცხვი ზუსტად იმდენია, რამდენი დიამეტრიც ჩაეტია ზემოთ, წრის სიგრძეში :)

ეს გასაკვირი არ არის, რადგან როგორც ვიცით, წრის რადიუსი, მისი დიამეტრის ნახევარია. ხოლო განმარტებასაც თუ გავიხსენებთ, მარტივად მივხვდებით, რომ ამ შემთხვევაშიც, ნახევარ წრეში პი-ცალი რადიანი ჩაეტევა.

GIF #3

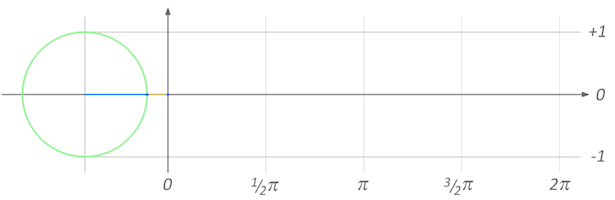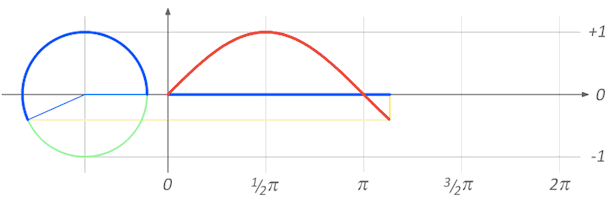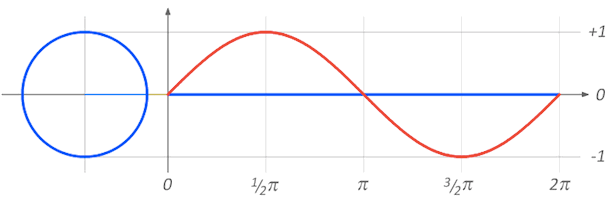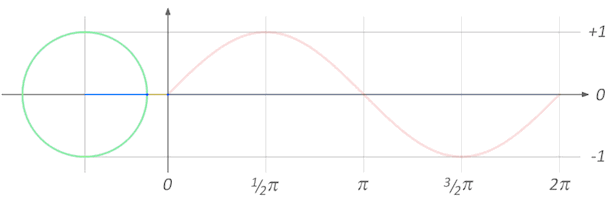
მესამე მეთოდი, რომლითაც წრის გარშემოწერილობის და მისი დიამეტრის შეფარდების სხვაგვარად წარმოდგენა შეგვიძლია, სინუსოიდაა. დახატული და მოციმციმე სინუსოიდა, სავარაუდოდ, ხშირად გინახავთ სამეცნიერო ფანტასტიკურ ფილმებში, ან, სამედიცინო დაწესებულებებში, ან, შეიძლება, სკოლაშიც კი, ტრიგონომეტრიის სწავლისას. სინუსოიდა სინუს-ფუნქციის აღმწერი ორგანზომილებიანი გრაფიკია. ეს ფუნქცია კი, რეალურად, ძალიან მარტივი რამეა — მართკუთხა სამკუთხედში, ჩვენთვის საინტერესო მახვილი კუთხის მოპირდაპირე კათეტის შეფარდება ჰიპოტენუზასთან (ანუ ის გვერდი, რომელიც მართკუთხა სამკუთხედში ყველაზე გრძელია).

როგორც ზედა GIF-დან ჩანს, სინუსოიდა ასევე შეგვიძლია წარმოვადგინოთ, როგორც კოორდინატები ერთეულოვან წრეწირზე და, როგორც კი ნახევარ წრეწირს „გავირბენთ”, ზუსტად π მანძილი გვექნება „გავლილი” სინუსოიდის აბსცისთა ღერძზე.

და ბოლოს — თუ ძალიან ცნობისმოყვარე ხართ და გაინტერესებთ, რა ციფრები მოდის 3,14-ის შემდეგ, ინებეთ პის პირველი ათასი სიმბოლო ათწილადის ნიშნის შემდეგ:

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989