კომპიუტერული მეცნიერებების საწყისები

მიუხედავად იმისა, რომ სიტყვა "კომპიუტერის" გაგონებისას ჩვენ თვალწინ ფიზიკური ობიექტი წარმოგვიდგება, რომლის მეშვეობითაც ფილმებს ვუყურებთ, სტატიებს ვწერთ ან თამაშებს ვთამაშობთ, დიდი ხნის მანძილზე კომპიუტერი თეორიული ცნება იყო.

მათემატიკაში და ლოგიკაში ახლაც ხშირად გამოიყენება ტერმინი "კომპუტაციური მოდელი" — ესაა აბსტრაქტული მოდელი, რომელიც ხსნის, როგორ გამოითვლება რაღაც (output), თავდაპირველად შეყვანილი მონაცემების საფუძველზე (input).

მეოცე საუკუნის დასაწყისში და 40-50-იან წლებში რეალური კომპიუტერები, რომლებიც რთულ გამოთვლებს ჩვენ გარეშე შეასრულებდნენ, ემბრიონალურ სტადიაზე იმყოფებოდნენ. დღევანდელი გადმოსახედიდან ეს აშკარაა. თუმცა იმის გამო, რომ იმდროინდელი გარღვევები კომპიუტერულ მეცნიერებაში (აქ კომპიუტერული მეცნიერების თეორიული მხარეც იგულისხმება) ძალიან იმედისმომცემი იყო, მკვლევრებმა კომპიუტერების (თეორიული თუ პრაქტიკული) მეცნიერების პრობლემების გადაჭრისთვის დაიწყეს ზრუნვა.

ერთი რამ, რაც კომპიუტერებს ჯერ კიდევ 40-50-იან წლებში რაღაც გაგებით ადამიანებზე უკეთ გამოსდიოდათ, დიდი რაოდენობის მონაცემთა ანალიზი იყო. ეს მეცნიერებისთვის მნიშვნელოვანი იმიტომაა, რომ, ერთი შეხედვით, მეცნიერება თითქმის მთლიანად მონაცემთა ანალიზია.

სამყარო სავსეა ქაოსური, არაორგანიზებული ინფორმაციით, რომელსაც მეცნიერები ახარისხებენ და მიზეზშედეგობრივი კავშირების გავლებით, გამოსავლიანობის წინასწარმეტყველებას ცდილობენ. რატომ არ შეიძლება იგივე გააკეთოს ჩვენ პატარა ბიოლოგიურ ტვინებზე ბევრად მძლავრმა კომპიუტერმა, რომელიც ყოველდღე უმჯობესდება?

ხელოვნური ინტელექტის და მანქანური დასწავლის განვითარების მცდელობები ნაწილობრივ ამ ამბიციიდან იწყება. ადამიანები საკუთარ თავებს სამყაროში ყველაზე ჭკვიან არსებებად მივიჩნევთ, კომპიუტერული მეცნიერების სპეციალისტებმა კი სწორედ ამ ფუნდამენტური რწმენის კითხვის ნიშნის ქვეშ დაყენება დაისახეს მიზნად. ამის მისაღწევად საუკეთესო საშუალება კი იმის ჩვენებაა, რომ "ადამიანურ" რაღაცებს — იქნება ეს გამოთვლა, ინფორმაციის შეგროვება, მეტყველება თუ წაკითხულის გააზრება — კომპიუტერი თავს ჩვენზე უკეთ ართმევს.

ამ სტატიაში ყურადღებას საკუთრივ მეტყველებაზე გავამახვილებთ, რადგან ადამიანური ენის რეპლიკაცია კომპიუტერული მეცნიერების და კომპუტაციური ლინგვისტიკის დარგში ერთ-ერთი, ჯერ კიდევ მიუღწეველი ამოცანაა. თუმცა ზოგი ასე არ თვლის. ამიტომ სკეპტიკოსებსაც შევეხებით.

ადამიანური ენის რეპლიკაციის ადრეული მცდელობები

ერთი შეხედვით, ნებისმიერი ენა ძალიან მარტივად შეგვიძლია აღვწეროთ. მაგალითად, შემიძლია ვთქვა, რომ ენა არის სიტყვებს შორის მიმართებებით შექმნილი ფრაზების და წინადადებების ერთობლიობა, რომლის მეშვეობითაც ადამიანები ერთმანეთს რაღაცებს (იქნება ეს აბსტრაქტული ფიქრები თუ, უბრალოდ, ფიზიკურ რეალობაზე დაკვირვებები) უზიარებენ.

ნებისმიერ ენაში, იქნება ეს ქართული თუ ინგლისური, ზოგი სიტყვა ერთმანეთთან "ჯდება" და ამიტომ მსგავსი სიტყვათშეთანხმებები ხშირად გამოიყენება. ზოგ შემთხვევაში კი გარკვეული სიტყვები ერთმანეთს ვერ მიესადაგება. მაგალითად, შემდეგი ფრაზა სავსებით ბუნებრივია: "ძალიან ლამაზი ბიჭი", თუმცა "ძალიან ბიჭი" არაგრამატიკულია და საუბრისას ან წერისას მსგავს ფრაზას იშვიათად შეხვდებით.

ენის კომპიუტერული სიმულაციის თავდაპირველი მცდელობები ენის ზემოხსენებულ მარტივ განმარტებას დაეყრდნო: დავახარისხოთ სიტყვები ჯგუფებად, სადაც ერთი ჯგუფის რომელიმე წევრი მეორე ჯგუფის რომელიმე წევრს მიესადაგება; მეორე ჯგუფის წევრი კი მესამეს წევრს მიესადაგება და ასე შემდეგ. ამ გზით, ყველა ჯგუფის ყველა წარმომადგენლის ერთმანეთთან მიერთება შეიძლება. ამგვარი სიტყვების ჯაჭვის აწყობა მარტივ კომპიუტერულ ხელსაწყოს ან მოდელსაც შეუძლია. ასეთ ხელსაწყოს ტექნიკური სახელი "სასრული მდგომარეობის მანქანა" (FSM) ან "მარკოვის მოდელი" ეწოდება.

მოდით, ცოტა ხანი კომპიუტერებს შევეშვათ და ასეთი თეორიული ხელსაწყო ჩვენით შევქმნათ: მაგალითად, სოციალური მეცნიერებების ჟარგონის გენერატორი. ამისათვის ავიღოთ სამი ჯგუფი და ყველგან ჩვენთვის სასურველი ის ტერმინები შევიტანოთ, რომლებიც სოციალურ მეცნიერებებში გვხვდება:

ჯგუფი 1

დიალექტური, პოზიტივისტური, სინქრონული, იტეგრირებული;

ჯგუფი 2

დეგენერაციული, აგრეგატული, სიმულირებული, პროგრესული;

ჯგუფი 3

დიფუზია, პერიოდულობა, ექვივალენტობა, ნეოლიბერალიზმი.

დააჭირეთ თქვენს წარმოსახვით კომპიუტერზე ღილაკს თითი და საინტერესო კომბინაციებს მიიღებთ. მაგალითად: "პოზიტივისტური დეგენერაციული ნეოლიბერალიზმი" ან "დიალექტური სიმულირებული პერიოდულობა". დიახ, შედეგად ისეთ ფრაზებს ვიღებთ, გეგონება, რომელიღაც ფრანგი სოციალისტი ფილოსოფოსის მონოგრაფს ვკითხულობთ.

სიტყვების ჯაჭვის ხელსაწყო დისკრეტული კომბინატურული სისტემის ყველაზე მარტივი მაგალითია. მსგავს სასრული მდგომარეობის მანქანას ქართული წინადადებების უსასრულოდ გენერირება შეუძლია.

მაგალითად, ჯგუფი 1(ლამაზი, ჭკვიანი, კეთილი), ჯგუფი 2 (ბედნიერი), ჯგუფი 3 (ბიჭი, გოგო, ძაღლი), ჯგუფი 4 (ჭამს) ჯგუფი 5 (ნაყინს, ორცხობილას, კაპიტალიზმის ტყუილებს). აქედან ბევრნაირი ჯაჭვის აწყობა შეიძლება: "ლამაზი ბედნიერი გოგო ჭამს ნაყინს", ან "ჭკვიანი, ბედნიერი ძაღლი ჭამს ორცხობილას" და ა.შ.

ენის მოდელირებისას შეგვიძლია, სიტყვების თანმიმდევრობის ალბათობაც გავითვალისწინოთ. თქვენი ტელეფონის კლავიატურა სწორედ ამ სისტემას იყენებს, როცა ის თითქოს ხვდება, რას დაწერთ შემდეგს (autocomplete).

განა, კომპიუტერი მართლა ლაპარაკობს

50-60-იან წლებში მეცნიერება ენის ზემოხსენებული მოდელირება გააკრიტიკეს. ყველაზე ნათლად ეს კრიტიკა ნოამ ჩომსკის 1957 წლის წიგნში, Syntactic Structures-ში ჩანს. ჩომსკის აზრით, მეტყველების შესწავლისადმი მსგავსი მიდგომა ძალიან არასწორი იყო და ადამიანურ ენასთან არაფერი ჰქონდა საერთო.

პირველ რიგში, ამ შესაძლოა, გრამატიკულად სწორი, მაგრამ სემანტიკურად რთულად წინასწარმეტყველებადი წინადადებები წარმოვთქვათ. მაგალითად, "უფერულ მწვანე იდეებს სძინავთ მძვინვარედ".

სიტყვების ჯაჭვის წარმომქმნელი მანქანა ნაკლებად იწინასწარმეტყველებს, რომ "უფერულს" "მწვანე" მოჰყვება, "იდეებს" კი — მძვინვარე ძილი. ამასთანავე, მარკოვის მოდელი მომდევნო სიტყვების ძიებისას რამდენიმე ვარიანტს უყურებს. დავუშვათ, ასეთი ხელსაწყოს გენერირებული პირველი სიტყვა არის "ლამაზი", შემდეგი ვარიანტები კი — "ბიჭი გარბის" ან "კაცი დახტის". ამის შემდეგ ჩვენმა ხელსაწყომ კიდევ უნდა იპოვოს სიტყვები, თუმცა რაც უფრო მეტ სიტყვას ამატებს წინადადებაში, მით უფრო ბუნდოვანი ხდება მთლიანად წინადადება. რატომ? ეს შეგვიძლია, ეგრეთ წოდებული ჰორიზონტის ეფექტით ავხსნათ.

ჰორიზონტის ეფექტის საილუსტრაციოდ შეიძლება, ჭადრაკი მოვიყვანოთ. ავიღოთ კომპიუტერი, რომელიც 4 სვლას წინასწარ ხედავს. ერთი სვლის გაკეთების შემდეგ სიტუაცია შეიცვლება და მომდევნო 4 სვლის დანახვისას კომპიუტერი მიხვდება, რომ თავდაპირველი სვლა არასწორი გამოდგა — ანუ მეხუთე სვლა მისი ხილვადობის ჰორიზონტს გასცდა.

მეტყველების მარკოვის ჯაჭვის მოდელირებისას იგივე ხდება. როცა ჩვენი ხელსაწყო წინადადების აწყობას იწყებს, ის "მომავალში" ვერ იყურება.

დავუშვათ, ჩვენ ხელსაწყოს დავავალეთ, რომ ააწყოს 10-სიტყვიანი წინადადება. ისიც დავუშვათ, რომ მას სიტყვების დალაგება წყვილებად შეუძლია: თავიდან წერს ორ სიტყვას, რომელსაც მიუსადაგებს მომდევნო ორ სიტყვას, საბოლოო ჯამში კი 4 სიტყვა გამოდის. როცა ჩვენი ხელსაწყო მეხუთე და მეექვსე სიტყვების ძებნას დაიწყებს, ისინი, შესაძლოა, თავდაპირველ 4 სიტყვას ცუდად მიესადაგებოდნენ.

რაც უფრო მეტად გავზრდით ასეთი ხელსაწყოს "ხილვადობას", ანუ მეტი სიტყვის დანახვის უნარს, მით მეტი მეხსიერება დასჭირდება მას.

სისტემის ალბათური ბუნების გამო, რაც უფრო დიდია წინადადება, მით უფრო რთულია მისი გამართულად აწყობა. ადამიანები საუბარს უშუალო სიტყვების თანმიმდევრობის დასწავლით კი არა, მას მიღმა არსებული პრინციპებით სწავლობენ.

დავუშვათ, უფრო ჭკვიანი ხელსაწყო შევქმენით, რომელიც ზემოხსენებულს ითვალისწინებს. პრობლემები აქ არ მთავრდება. მაგალითად, ავიღოთ წინადადება:

ან გოგო ჭამს ნაყინს, ან ის ჭამს კანფეტს; თუ გოგო ჭამს ნაყინს, მაშინ ბიჭი ჭამს ნამცხვარს.

სიტყვების ჯაჭვების მაგენერირებელი ხელსაწყო წინადადებებში არსებულ სივრცით მიმართებებს ვერ აღიქვამს. თუ წინადადების დასაწყისში კომპიუტერს აღარ "ახსოვს", წინადადების დასაწყისში რომ "თუ" დაწერა და როცა წინადადებაში "ან/მაშინ"-ის ჯერი მოვა, ის წინადადებას არასწორად დაწერს. შეიძლება, ამ პრობლემას გვერდი ავუაროთ და ჩვენი მოდელი უფრო დავხვეწოთ, რისი დახმარებითაც ის დაიმახსოვრებს წინადადების დასაწყისში დაწერილ სიტყვას, რათა მოგვიანებით გამოყენებული სიტყვები შესაბამისობაში იყოს მათთან. ეს უკვე ძალიან დიდ გამომთვლელ ძალას მოითხოვს.

საბოლოო პრობლემა კი ისაა, რომ კომპიუტერს რთული — თანწყობილი თუ ქვეწყობილი — წინადადებების გაგება უჭირს. ეს ისეთი წინადადებებია, რომლებიც რამდენიმე ფრაზას შეიცავენ:

თუ გოგო ან ნაყინს შეჭამს, ან კანფეტს, მაშინ ბიჭი ნამცხვარს შეჭამს;

თუ გოგო ნაყინს შეჭამს, შემდეგ ბიჭი ნაყინს შეჭამს / თუ გოგო ნაყინს შეჭამს, მაშინ ბიჭი ნამცხვარს შეჭამს.

თუ/მაშინ-ის გამოყენებას წინადადებაში ლიმიტი არ აქვს. შესაბამისად, კომპიუტერს რომ ყოველ ჯერზე დავამახსოვრებინოთ, როდის უნდა ჩასვას ეს სიტყვები, ამისთვის მას უსასრულო მეხსიერება დასჭირდება.

ამას ემატება ისიც, რომ ენაში სიტყვების თანმიმდევრობის ალბათობის გამოცნობა მცირე როლს თამაშობს და ის არაფერს ამბობს უშუალოდ ენის სტრუქტურაზე და მის ნიშან-თვისებებზე.

ჩომსკის იერარქია და პროგრამული ენები

ადამიანური ენა თავისებური კომპუტაციური სისტემაა. მავანი ლექსიკონიდან (მარტივად რომ ვთქვათ, ესაა სიტყვების მარაგი) ინფორმაციას არჩევს, შემდგომ ეს ინფორმაცია გარკვეული სისტემით ორგანიზდება და გადმოიცემა ფრაზების ან წინადადების სახით.

უშუალოდ ადამიანური ენის კვლევამდე ნოამ ჩომსკიმ ადამიანური და არაადამიანური ენების კლასიფიკაცია იერარქიულად მოახდინა. შეგვიძლია, მოვიგონოთ ენა, რომელშიც მხოლოდ ორი სიმბოლოა: a და b. აქვე ამ ენას შეგვიძლია მოვუფიქროთ გრამატიკა. მაგალითად, წარმოვიდგინოთ ისეთი ენა, სადაც ყველა წინადადება a-თი იწყება და აქვე მთავრდება ან შემდგომ ba მოსდევს. წინააღმდეგ შემთხვევაში, ენა გრამატიკულად გაუმართავია. ასეთი ენა შეგვიძლია სასრულ ავტომატად აღვწეროთ. არ დაიბნეთ, ყველაფერს განვმარტავ:

აუტომატათა თეორია აბსტრაქტული მანქანების სწავლას ეწოდება, რომელიც მიზნად კომპუტაციური პრობლემის გადაჭრას ისახავს მიზნად. სასრული მდგომარეობის აუტომატა ავტომაციის ერთ-ერთი უმარტივესი მოდელია. აუტომატა გარკვეული input-ის შემთხვევაში გადადის სხვა მდგომარეობაში, რომელიც დამატებით ააქტიურებს სხვა მდგომაროებას და შედეგად ან output-ს ვიღებთ, ან ერთი და იგივე პროცესი მუდმივად მეორდება.

სასრული აუტომატას რეალური მაგალითი სავაჭრო ავტომატია. თუ მასში ჩააგდებთ ფულს, ის აქტიურდება; შეიყვანთ მასში სასურველ რიცხვს და ის შემდეგ "მდგომარეობაში" გადადის; პოულობს რიცხვის შესაბამის პროდუქტს, რომელსაც გადმოგიგდებთ. ამის მერე, ის საწყის მდგომარეობას უბრუნდება და მზადაა, ახალი შეკვეთა მიიღოს.

ჩვენი მოგონილი ენის შემთხვევაში, თუ სასრული მდგომარეობის აუტომატამ წინადადების თავში დაინახა a სიმბოლო, შეიძლება ითქვას, რომ ის გააქტიურდა. თუ მან დაინახა b, მაშინ ის არ გააქტიურდება, რადგან ეს ჩვენი ენის წესებს ეწინააღმდეგება: პირველი სიმბოლო აუცილებლად a უნდა იყოს. ამასთან, თუ მომდევნო სიმბოლოც a არის, მაშინ ის შეჩერდება.

ჩვენი გრამატიკის აუტომატა ასე გამოიყურება:

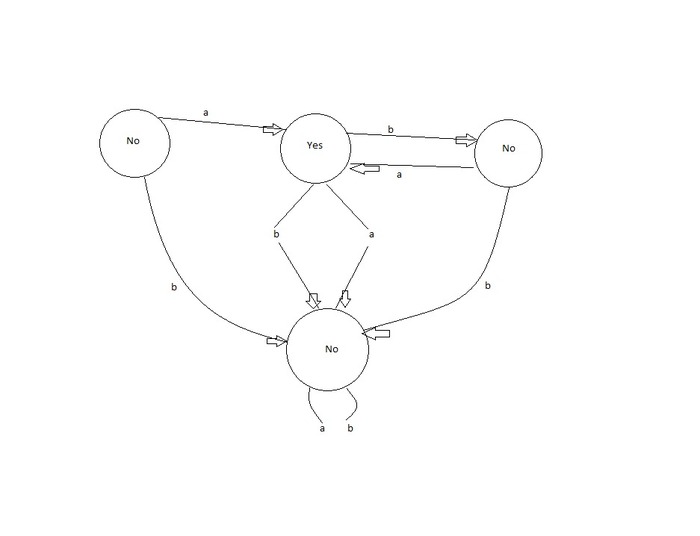
მოდით, განვიხილოთ, რას ვუყურებთ გამოსახულ გრაფაზე: თავდაპირველად, აუტომატა არააქტიურია, რადგან მას სიმბოლო არ მიუღია. თუ ის თავდაპირველად იღებს a სიმბოლოს, აუტომატა აქტიურდება და გადადის Yes მდგომარეობაში. თუ ის თავიდანვე b-ს იღებს, მაშინ ის არ აქტიურდება და გადადის No მდგომარეობაში. გააქტიურების შემთხვევაში, როცა მან ერთი a უკვე მიიღო, შემდეგ ის იღებს b-ს, თუმცა მომდევნო მდგომარეობაში მას b-ს და a-ს მიღება სჭირდება, ამიტომ კიდევ No მდგომარეობაში გადადის, თუმცა თუ b-ს მერე კიდევ a-ს მიიღებს, პირობა შესრულდა და აუტომატა Yes მდგომარეობას დაუბრუნდება.

ახლა ჩვენი ენის ფორმალური წარმოსახვაც შეგვიძლია:

L= , სადაც a და b ენის კომპონენტებია, ხოლო L ჩვენი ენა. უშუალოდ გრამატიკა კი შემდეგნაირად შეგვიძლია დავწეროთ:

S → aX

X → baX|ε

სადაც S საწყის მდგომარეობას აღნიშნავს. a-ს "დანახვის" შემთხვევაში აუტომატა შემდეგ მდგომარეობაში, X-ში გადადის. თუ ეს განხორცელდა, და ეს უკვე დასრულებული წინადადებაა (ამას ეპსილონი აღნიშნავს), რადგან, როგორც ვთქვით, ჩვენი გრამატიკის წესები მხოლოდ a-ს ან a-ს შემდეგ ba-ის თანმიმდევრობას ითვალისწინებს.

ეს შეგვიძლია გავამარტივოთ და შემდეგნაირად ჩავწეროთ: S → Sba|a

ანუ საწყის მდგომარეობაში (S) აუტომატას შეხვდა a და გაჩერდა, ან შეხვდა შემდეგ მდგომარეობაში გადასვლისთვის აუცილებელი სიმბოლო (მეორე S, ამ შემთხვევაში a), რომელსაც მოჰყვება ba.

ასეთ გრამატიკას "რეგულარული" გრამატიკა ეწოდება, რომელსაც სასრული მდგომარეობის აუტომატა აღწერს. ამას გარდა, არსებობს ენები, რომლებსაც აღწერს "არადეტერმინისტული", "წრფივად განსაზღვრული არადეტერმინირებული ტურინგის მანქანა" და "ტურინგის" მანქანა. ანუ ესენია მეორე ტიპის (კონტექსტდამოუკიდებელი), პირველი ტიპის (კონტექსტსენსიტიური) და ნულოვანი (რეკურსიულად აღწერადი) ტიპის გრამატიკები.

თითოეულის განხილვა ამ სტატიისთვის საჭიროა არ არის. ზემოხსენებული მაგალითი იმის საილუსტრაციოდ მოვიყვანე, რომ ენა მხოლოდ ადამიანური სამეტყველო ენა კი არაა — როგორებიცაა, მაგალითად, რუსული ან ფრანგული — არამედ, სიმბოლოების ნებისმიერი სინტაქსური ურთიერთქმედება, რომელიც გარკვეულ წესებს ემორჩილება.

ამ კატეგორიზაციამ ხელი სხვადასხვა პროგრამული ენის ჩამოყალიბებას შეუწყო. ისინი სწორედ ზემოხსენებული ტიპის ენებია: იქნება ეს C++ თუ Java.

თუმცა პროგრამული ენების გარდა, მეცნიერებმა მსგავსი კატეგორიზაციის ღირებულება ადამიანური ენის შესწავლისთვისაც დაინახეს. კერძოდ, თუ დადგინდება, ზემოხსენებული ენებიდან სად შეიძლება ჩაჯდეს ნებისმიერი ადამიანური ენა, მაშინ შეგვიძლია, მის მიღმა არსებული აბსტრაქტული პრინციპები უკეთ შევისწავლოთ და ადამიანური ენა სწორედ ამ პრინციპებზე დაყრდნობით ვაწარმოოთ.

ენების უნივერსალური გრამატიკა

მიუხედავად იმისა, რომ ენებს შორის სხვაობები არსებობს, ყველა ენას აქვს საერთო მახასიათებლები. კერძოდ, სამი მახასიათებლის გამოყოფა შეიძლება. ესენია: რეკურსიულობა, უნიტარულობა და შეერთების პრინციპი.

ყველა ადამიანური ენა რეკურსიულია. იმისთვის, რომ ვნახოთ, რას ნიშნავს ეს, მაგალითი მოვიშველიოთ: ავიღოთ წინადადება, "მე ვარ ჟურნალისტი". ის შეგვიძლია ჩავსვათ სხვა წინადადებაში: "ქეთიმ თქვა, რომ მე ვარ ჟურნალისტი". ამავე პრინციპით შეგვიძლია ვთქვათ: "ნინიმ თქვა, რომ ქეთიმ თქვა, რომ მე ვარ ჟურნალისტი". ამის გაგრძელება უსასრულოდ შეიძლება. ისეთი ენა რომც არსებობდეს, სადაც რეკურსია არ გამოიყენება, იმ ენაზე მოსაუბრე ადამიანებს ექნებათ უნარი, რომ რეკურსიული წინადადებები წარმოთქვან.

ადამიანური ენა უნიკალური იმითია, რომ ის უნიტარულია. რას ნიშნავს ეს? მაგალითად, ადამიანის მიერ წარმოთქმული წინადადება შეგვიძლია აღვწეროთ ნატურალური რიცხვებით (სიტყვების რაოდენობა). "მე მქვია ტატო" სამ ცალკეულ სიტყვას შეიცავს, სადაც სამივე რაღაცას მიემართება. ცხოველების კომუნიკაციის იმავენაირად აღწერა შეუძლებელია.

შეერთების პრინციპი (merge) აღწერს ორი სინტაქსური ობიექტის შეერთებას, რომელიც ახალ სინტაქსურ ობიექტს წარმოქმნის. ესეც ადამიანური ენის მახასიათებელია.

ეს წესები ყველა ენაში გვხვდება და ნოამ ჩომსკი ვარაუდობს, რომ ადამიანები სწორედ ამ წესებით (და კიდევ დამატებით წესებით, თუმცა ეს უკვე საკამათოა) ვიბადებით და მაშასადამე, ენის ათვისებასაც სწორედ ასე ვახერხებთ.

აქ მნიშვნელოვანი კითხვა ისმის: შეუძლია თუ არა კომპიუტერს ზემოხსენებული წესების გათვალისწინებით ენის და გამართული მეტყველების წარმოება?

შეძლებს თუ არა ხელოვნური ინტელექტი ქართულად ლაპარაკს

ადამიანური ენების რეპლიკაციის მთავარი პრობლემა მისი კონტექსტ-დამოკიდებულებაა. იმის მიხედვით, თუ რა შინაარსს გამოხატავს წინადადება, სიტყვათა თანმიმდევრობა იცვლება. მაგალითად, გადავიყვანოთ შემდეგი თხრობითი წინადადებები კითხვით ფორმაში:

(1) კატა ზის.

(1.1) კატა ზის?

(2) კაცი რომელიც მაღალი არის, სევდიანი არის.

(2.1) არის კაცი, რომელიც მაღალი არის, სევდიანი?

პირველი მაგალითი საკმაოდ მარტივია. ხელოვნური ინტელექტი მარტივად მიხვდება, როგორ უნდა გადაიყვანოს (1) კითხვით ფორმაში. თუმცა (2)-ის კითხვით ფორმაში გადაყვანა ბევრად რთულია. დააკვირდით, (2.1)-ში როგორ იცვლება ზმნა "არის"-ის ადგილმდებარეობები წინადადებაში.

ერთი "არის" კაცის სიმაღლეს მიემართება, ხოლო მეორე მის სევდიანობას აღწერს. მიუხედავად ამისა, მეორე "არის" წინადადების დასაწყისში გადაადგილდა, ხოლო სიმაღლესთან მიმართებაში მყოფი "არის" ადგილზე დარჩა. კომპიუტერისთვის მსგავსი გადანაცვლება რთულია, რადგან ისეთი წესი არ არსებობს, რომელიც, მაგალითად, გვეტყვის, რომ ყოველ მეორე არსებით სახელთან მყოფი ზმნა კითხვით ფორმაში წინადადების დასაწყისში უნდა გადავიდეს.

წინადადებებში სიტყვები წრფივად არ გადანაცვლდება. ანუ სამეტყველო ენებში ისეთი წესი არ მოქმედებს, სადაც, მაგალითად, კითხვით ფორმაში გადაყვანისას, პირველი ზმნა წინადადების დასაწყისში აღმოჩნდება. ამ შემთხვევაში წინადადების დასაწყისში ყველაზე "შორეული" ზმნა გადადის.

მსგავსი გადანაცვლებები სხვანაირ სიმეტრიის წესებს ეფუძნება, რომლის ბუნებაც შესწავლილი არ არის. სამწუხაროდ, ხელოვნური ინტელექტით გენერირებული წინადადებები ისევ მარკოვის ჯაჭვებს ეფუძნება.

მაგალითად აიღეთ გარდიანის ეს სტატია, რომელიც ხელოვნურმა ინტელექტმა GPT-3-მა დაწერა. ის ძალიან შეზღუდულია. აი, რატომ:

დავუშვათ, ასეთ ხელოვნური ინტელექტის ბოტს მიეცით რაღაც ინფორმაცია (input), რომელიც მან უნდა "გაიგოს" სემანტიკურად, სინტაქსურად და კონტექსტუალურად. ამას ის ისევ მარკოვის ჯაჭვების გამოყენებით ახერხებს. იმისთვის, რომ პროგრამა ერთი მდგომარეობიდან შემდეგში გადავიდეს, ტექსტის წერასთან ერთად, მას ინფორმაცია უნდა ახსოვდეს. იმისთვის, რომ მან ეს დაიმახსოვროს და ტექსტი ბუნებრივი ჩანდეს, მას დიდი მეხსიერება სჭირდება.

დავუშვათ კომპიუტერს დაავალეთ, რომ დაწეროს "სცენარი" და საამისოდ მას ასობით სხვადასხვა სცენარის ფილმი მიეცით. ეს შედეგის მისაღწევად საკმარისი მაინც არ იქნება და ბოტი ზოგ მომენტში ძალიან უცნაურ რაღაცებს დაწერს (არა რაღაც კაუფმანურ უცნაურს, არამედ უაზრობას), რადგან საბოლოო ჯამში კომპიუტერის მიერ სცენარის დაწერის ან ლაპარკის პროცესი, ფუნდამენტურ დონეზე, ადამიანურისგან ძალიან განსხვავდება.

ადამიანური ენების უნივერსალური გრამატიკის მახასიათებლების ხელოვნური ინტელექტისთვის სწავლება ძალიან რთულია, რადგან ისინი არასათანადოდ კარგად განსაზღვრული აბსტრაქტული ცნებებია, რომელიც კომპიუტერს "არ ესმის". უკეთ რომ ავხსნა რას ვგულისხმობ: დავუშვათ მაქვს ძალიან მძლავრი კომპიუტერი, რომელზეც ვიდეოკამერა და თერმული დეტექტორებია მიმაგრებული. ეს კომპიუტერი კი ფანჯრიდან იყურება: ხედავს როგორ ცვივა ფოთლები, როგორ უბერავს ქარი, როგორი ამინდია და ა.შ.

ასეთი კომპიუტერი, რომელსაც ძალიან ძლიერი პროცესორი აქვს, ადამიანზე უკეთ იწინასწარმეტყველებს, რა მოხდება ხვალ მისი ხილვადობის არეში. ადამიანმა მსგავსი რამ რომ სცადოს, უაზრობაც კია. თუმცა, ეს კომპიუტერი ვერ მიაგნებს ფიზიკის კანონებს, რომლებიც ამ მოვლენებს განსაზღვრავენ.

ხელოვნურ ინტელექტს ადამიანური მახასიათებლების იმიტაცია და მონაცემებზე დაყრდნობით ალბათური მოდელების აგება კარგად გამოსდის. თუმცა, მეცნიერებს აქვთ ეჭვი, რომ ეს ალბათური მოდელები საკმარისი არაა.

იმ შემთხვევაშიც კი, თუ ხელოვნური ინტერელქტი ისე განვითარდა, რომ მის ნაწერს ან "ნალაპარაკებს" ადამიანურისგან ვერ გავარჩევთ, მთავარი კითხვა, თუ როგორია ადამიანური ენის და მეტყველების ფუნდამენტური ბუნება, პასუხგაუცემელი რჩება.