როგორია შავი ხვრელების აღსასრული? — ახალი კვლევა მათი სიკვდილის სხვაგვარ სცენარს გვთავაზობს

ფოტო: Event Horizon Telescope Collaboration
შავი ხვრელები სამყაროში ყველაზე იდუმალი ობიექტებია, რომელთა წარმოქმნისა და სიკვდილის დეტალებიც ჩვენთვის ჯერ კიდევ ბუნდოვანებითაა მოცული. ფიზიკოს სტივენ ჰოკინგის მეშვეობით, გავიგეთ, რომ ისინი საბოლოოდ "ორთქლდება" და კოსმოსიდან პოტენციურად ქრება, თუმცა გრავიტაციასა და კვანტურ მექანიკაში ჩვენი ცოდნა ლიმიტირებულია, რაც მათი სიცოცხლის დასასრულის ბოლომდე გაგებას აძნელებს.
სანამ ახალ კვლევაზე გადავალთ, გეტყვით, რომ 1970-იან წლებში ზემოხსენებულმა მეცნიერმა სცადა, გაერკვია, რა ხდება შავი ხვრელების მიჯნაზე, რომელსაც მოვლენათა ჰორიზონტი ეწოდება. ჰოკინგის რადიაციის თეორიის თანახმად, სამყაროს კვანტური ველებისა და მოვლენათა ჰორიზონტის ურთიერთქმედება ერთგვარ გზას კვალავს, რომლითაც შავი ხვრელებს ენერგია აღწევს თავს, ნელა მოძრავი ნაწილაკებისა და რადიაციის ფორმით. ამ პროცესში ეს ობიექტები მასას კარგავს, პატარავდება და ქრება.
თუმცა, ამ თეორიასთან ერთად გაჩნდა შავი ხვრელის ინფორმაციული პარადოქსიც. საქმე იმაშია, რომ ინფორმაცია, რომელიც აღნიშნულ ობიექტებში ჩამავალ მატერიას შეესაბამება, მოვლენათა ჰორიზონტს ლახავს, მაგრამ უკან აღარასდროს ბრუნდება, არც რადიაციის სახით, ამიტომ გაურკვეველია, რა ემართება მას.
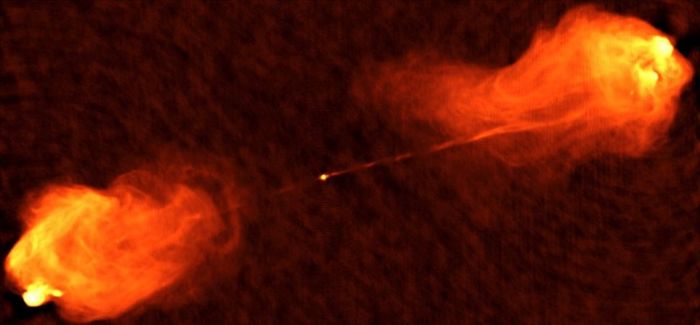
კაშკაშა რადიოწყარო "გედი А".
ფოტო: NRAO/AUI
ყველაზე მარტივი საშუალება, რომ ეს პარადოქსი ამოვხსნათ, აინშტაინის ფარდობითობის თეორიის "გადალახვა" და გრავიტაციის ახალი თეორიის შექმნაა, რადგან პირველი მათგანი შავი ხვრელის ცენტრთან მიმართებაში უკვე აღარ მუშაობს. საუბარია სინგულარობაზე, სადაც სიმკვრივე უსასრულო ხდება და მის აღსაწერად კვანტურ მასშტაბებზე გათვლილი გრავიტაციული პროცესები გვჭირდება.
სინგულარობას, რა თქმა უნდა, პირდაპირ ვერ შევისწავლით, მაგრამ ჰოკინგის რადიაციის წყალობითა და სიმების თეორიის გათვალისწინებით მსჯელობა შეგვიძლია. შედეგად ფარდობითობის მოდიფიცირებულ ვერსიებს ვიღებთ, რომლებითაც გავაანალიზებთ, როგორ შეიძლება "იქცეოდეს" გრავიტაცია, როცა კვანტურ ლიმიტს სულ უფრო და უფრო უახლოვდება, ანუ როცა მოვლენათა ჰორიზონტსა და შავი ხვრელის ცენტრს შორის ზღვარი მცირდება.
მეცნიერებმა ახალ კვლევაში აინშტაინ-დილატონ-გაუს-ბონეს გრავიტაციის თეორია გამოიყენეს, რომლის მთავარი არსიც ისაა, რომ შავ ხვრელებს მინიმალური მასა აქვს, რაც იმის გაგების საშუალებას იძლევა, თუ რა ემართება შავ ხვრელებს ამ მასასთან მიახლოებისას.
ზოგ შემთხვევაში, რაც თეორიის ბუნებასა და შავი ხვრელების ევოლუციაზეა დამოკიდებული, "აორთქლების" პროცესის შედეგად მიკროსკოპული ნაწილი რჩება, რომელსაც მოვლენათა ჰორიზონტი აღარ გააჩნია, წარმოუდგენლად ეგზოტიკურია და ინფორმაციის შენარჩუნება შეუძლია, რაც პარადოქსს ხსნის.
მეორე ვარაუდი ის გახლავთ, რომ შავი ხვრელი მინიმალურ მასას აღწევს და მოვლენათა ჰორიზონტი ეცლება, მაგრამ სინგულარობას მაინც ინარჩუნებს. ზოგადი ფარდობითობის მიხედვით, ასეთი "შიშველი სინგულარობა" ვერ იარსებებს, თუმცა ნამდვილად ასე რომ იყოს, ეს კვანტური გრავიტაციის სამყაროში გამავალ ფანჯარას გააღებდა.
ჯერჯერობით უცნობია რამდენად სწორ გაზე გავყავართ აინშტაინ-დილატონ-გაუს-ბონეს გრავიტაციის თეორიას, მაგრამ ეს მაინც წინ გადადგმული მნიშვნელოვანი ნაბიჯია. ავტორთა ნაშრომი სამეცნიერო პორტალ arXiv-ზეა ხელმისაწვდომი.











კომენტარები