კვანტური ექსპერიმენტებიდან ნობელის პრემიამდე — ფიზიკის დარგში წლევანდელ ლაურეატთა მიღწევები
ცოტა ხნის წინ ცნობილი გახდა, რომ ფიზიკის დარგში ნობელის პრემიის მფლობელები წელს ალენ ასპე, ჯონ კლაუზერი და ანტონ ცაილინგერი გახდნენ, რომელთაც ჯილდო "გადაჯაჭვული ფოტონების გამოყენებით ჩატარებული ექსპერიმენტებით, ბელის უტოლობის დარღვევითა და კვანტური ინფორმაციის მეცნიერებაში პიონერობით" დაიმსახურეს.
მათ თავიანთი კვლევებით გადაჯაჭვული ნაწილაკების შესწავლისა და კონტროლის პოტენციალი აჩვენეს. მაშინაც კი, როცა ასეთი ნაწილაკების წყვილი ერთმანეთისგან დაშორებულია, მაინც საერთო კვანტურ მდგომარეობას იზიარებს. ამ პროცესის შესახებ მეტის გაგება კვანტური ტექნოლოგიების (კომპიუტერები, ინტერნეტი, საკომუნიკაციო სისტემები და სხვა) განვითარების ახალ ერას უყრის საფუძველს.
ყოველდღიური გამოცდილებებისგან შორს
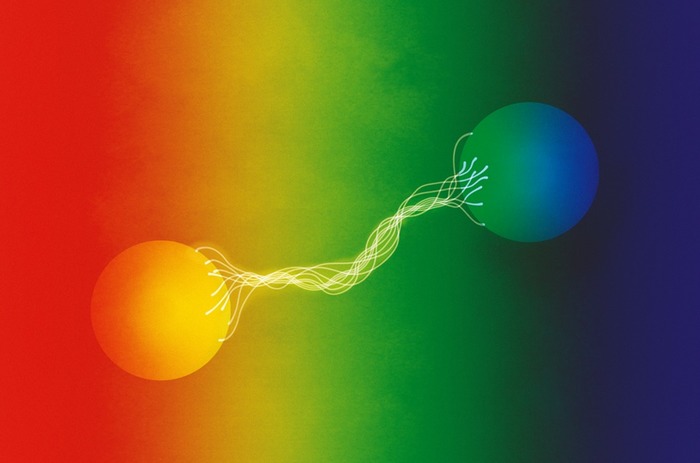
ნაწილაკების გადაჯაჭვულობისას, მხოლოდ ერთ-ერთი მათგანის მახასიათებლების გაზომვით შესაძლებელია, რომ მისი მეწყვილის ანალოგიური მახასიათებლები გამომავლინოთ. ამისთვის მეორე ნაწილაკზე ცალკე დაკვირვება არ გვჭირდება.
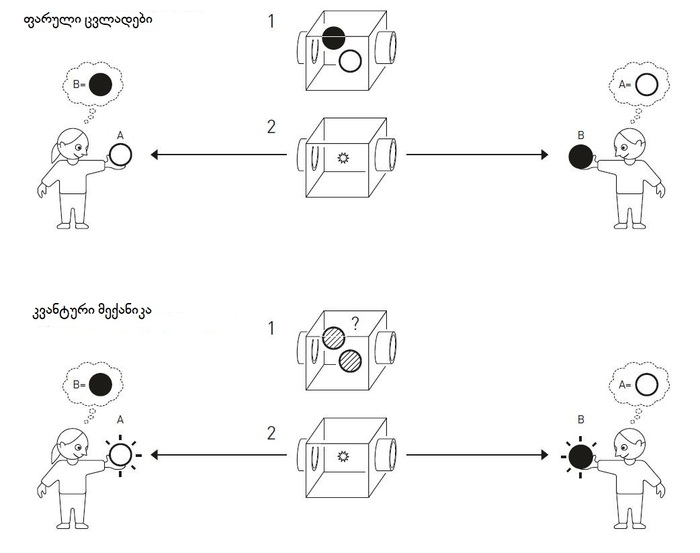
კვანტური მექანიკის განსაკუთრებულობა იმაში მდგომარეობს, რომ ბურთების მისეულ ეკვივალენტებს განსაზღვრული მდგომარეობა არ აქვს, სანამ არ გაზომავ. თითქოს, ორი ბურთი ნაცრისფერია იმ მომენტამდე, როცა მათ ვიღაც შეხედავს, შემდეგ კი შესაძლოა, შავი ან თეთრი გახდეს. მეორე მათგანი მაშინვე საპირისპირო შეფერილობას მიიღებს.
როგორ უნდა გავიგოთ, ჰქონდა თუ არა თითოეულს ეს ფერი თავიდანვე? მაშინაც კი, როცა ისინი ნაცრისფრად გვეჩვენება, შესაძლებელია, მათში ფარული "ინსტრუქცია" იყოს, რომელიც განსაზღვრავს, რა ფრად უნდა იქცეს ბურთი, როცა ვინმე შეხედავს.
არსებობს კი ფერი, როცა ობიექტს არავინ აკვირდება?
კვანტური მექანიკა შეიძლება შევადაროთ მოწყობილობას, რომელიც განსხვავებული შეფერილობის ბურთებს ურთიერთსაპირისპირო მიმართულებით ისვრის. თუ, მაგალითად, ხატია შავ ბურთს დაიჭერს, მიხვდება, რომ დათოს თეთრი ხვდა წილად. ჯონ სტიუარდ ბელის თეორიის მიხედვით, რომელიც ცვლადებს იყენებს, ბურთებში არსებული ფარული ინფორმაცია მათ ფერს განსაზღვრავს.
ამის მიუხედავად, კვანტური მექანიკა ამბობს, რომ ისინი ნაცრისფერი იყო, სანამ ვინმე შეხედავდა, შემდეგ კი შემთხვევითობის პრინციპით შავად და თეთრად იქცა. ბელის უტოლობები აჩვენებს, რომ ექსპერიმენტებით ამ მოცემულობებს შორის სხვაობის გაგება შეგვიძლია. მათი მეშვეობით დამტკიცდა, რომ კვანტურ მექანიკისეული აღწერა სწორია.
ფოტო: The Nobel Prize
ფიზიკის დარგში წლევანდელ ნობელიანტთა კვლევები სწორედ ბელის უტოლობების მცდარობას ავლენს და ცხადყოფს, რომ გადაჯაჭვულ ნაწილაკებში კვანტური განუსაზღვრელობა მუშაობს და არა ფარული ცვლადები. ეს იმას ნიშნავს, რომ ბუნება ისე "იქცევა", როგორც ამას კვანტური მექანიკა წინასწარმეტყველებს.
კვანტური მექანიკის ყველაზე მნიშვნელოვანი რესურსი
როცა საპირისპირო მიმართულებით მოძრავი ორი გადაჯაჭვული კვანტური ნაწილაკიდან ერთ-ერთი მესამესთან იკვეთება და მასთან გადაიჯაჭვება, ეს წყვილი საერთო ახალ მდგომარეობაში გადადის. მესამე ნაწილაკი "იდენტობას" კარგავს, თუმცა მისი ორიგინალური მახასიათებლები მეწყვილეში გადადის, რასაც კვანტური ტელეპორტაცია ეწოდება. ამის სადემონსტრაციო ექსპერიმენტი პირველად ანტონ ცაილინგერმა 1997 წელს ჩაატარა.
კვანტური ტელეპორტაცია სისტემიდან სისტემაში კვანტური ინფორმაციის დანაკარგის გარეშე გადატანის ერთადერთი საშუალებაა, რადგან კვანტური სისტემა ერთდროულად მრავალ მახასიათებელს აერთიანებს. რომელი იჩენს თავს დაკვირვებისას, წინასწარ ვერ განვსაზღვრავთ. როგორც კი ის ცნობილი გახდება, სხვა ყველა ვერსია ქრება.
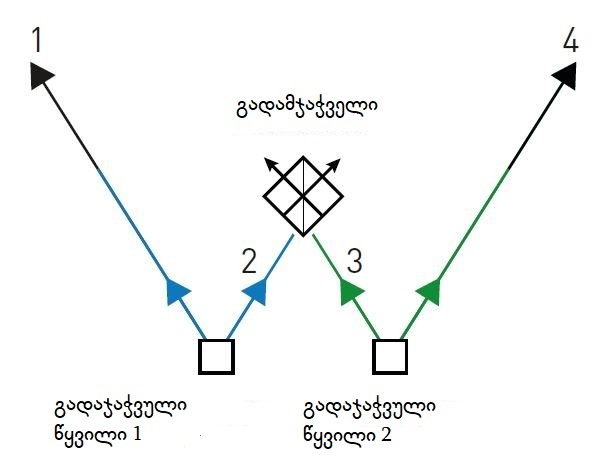
1998 წელს ცაილინგერის გუნდმა ნაწილაკების 2 წყვილი გამოიყენა, რომელთაგანაც თითო ერთმანეთთან გადაიკვეთა, რამაც დარჩენილი 2 ნაწილაკის საერთო მდგომარეობაში გადასვლა განაპირობა. კვანტურ ქსელში ოპტიკური ბოჭკოების მეშვეობით ასეთი გადაჯაჭვული ფოტონების საპირისპირო მიმართულებით, სიგნალის სახით გაშვება და წყვილების კავშირით ქსელის "კვანძებს" შორის მანძილის გაზრდაა შესაძლებელი, თუმცა არა უსასრულოდ.
ფოტო: The Nobel Prize
პარადოქსიდან უტოლობამდე
ყოველივე ზემოხსენებული ბუნებისა და რეალობის ურთიერთქმედების ჩვეულებრივ გაგებას ეწინააღმდეგება. ანუ ძნელი წარმოსადგენია, რა გავლენა უნდა იქონიოს სადღაც შორს მომხდარმა მოვლენამ რამეზე ისე, რომ იქიდან მომავალ სიგნალთანაც კი არ ჰქონდეს შეხება.
ეს არათუ რიგითი ადამიანისთვის, არამედ აინშტაინისთვისაც გაუგებარი იყო, რომელმაც ბორის პოდოლსკისთან და ნათან როზენთან ერთად დაასკვნა, რომ კვანტური მექანიკა რეალობის სრულფასოვან აღწერას არ გვთავაზობს. ამას აინშტაინ-პოდოლსკი-როზენის პარადოქსი ეწოდება.
მთავარი კითხვა გახლდათ: არის თუ არა სხვა აღწერა, სადაც კვანტური მექანიკა მხოლოდ ერთ-ერთი ნაწილია. ბელის თეორემის მიხედვით, ექსპერიმენტთა მრავალი სერიით ამის გარკვევა შესაძლებელია, რადგან შედეგების თანაფარდობა გარკვეულ ზღვარს ვერ გადააჭარბებს.
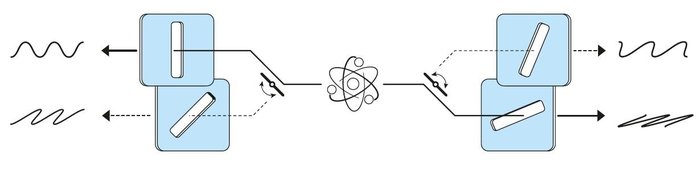
ჯონ კლაუზერი ბელის ამ იდეით დაინტერესდა და კოლეგებთან ერთად ექსპერიმენტით მისი გამოცდა გადაწყვიტა. მათ გადაჯაჭვული ფოტონების წყვილი საპირისპირო მიმართულებით გაუშვეს. ამ დროს პოლარიზაციის მიმართულება უცნობია, ვიცით მხოლოდ ის, რომ ნაწილაკების პოლარიზაცია პარალელურია. ამაზე დაკვირვების საშუალებას სპეციალური ფილტრები იძლევა.
თუ ორივე ნაწილაკს ფილტრისკენ ერთნაირ სიბრტყეზე გავუშვებთ და ერთი მათგანი მასში გაივლის, მეორის შემთხვევაშიც ასე მოხდება, ხოლო თუ წყვილი ერთმანეთის მიმართ კონკრეტული კუთხით იმოძრავებს, ერთ-ერთი გაჩერდება. რამდენჯერ მოხდება ეს, ფილტრების განლაგებაზეა დამოკიდებული.
კვანტურ მექანიკას გაზომვის შედეგების თანაფარდობამდე მივყავართ და ის ბელის უტოლობას არღვევს.
დარღვეული უტოლობა
ეს ექსპერიმენტი ჯონ კლაუზერმა 1972 წელს განახორციელა, რისთვისაც სპეციალური მოწყობილობა ააგო. მომდევნო წლებში ის და მისი კოლეგები ამ ცდის შეზღუდვებს, ანუ შესაძლო მცდარობას განიხილავდნენ. მაგალითად, იქნებ, მან როგორღაც მძლავრი თანაფარდობის მქონე ნაწილაკები გამოავლინა, სხვები კი — ვერა?
ამის გასარკვევად, ალენ ასპემ ახალი, გაუმჯობესებული მოწყობილობა შექმნა, რომლითაც ფილტრში გავლილი და შეჩერებული ნაწილაკების დაფიქსირება, ანუ უფრო მეტი ფოტონის გაზომვა შეიძლებოდა.
დასკვნით ცდებში მან გადაჯაჭვული ფოტონების მიმართულება მას შემდეგ შეცვალა, რაც ისინი პირველადი წყაროდან გაუშვა. ფილტრებს მხოლოდ 6 მეტრი აშორებდა, ამიტომ ეს ცვლილება წამის მემილიარდედში უნდა მომხდარიყო. თუ საწყის წყაროს ჰქონდა გავლენა, რომელ ფილტრში გაივლიდა ფოტონი, მაშინ ცვლილების შემდეგ იმავე ფილტრამდე ვეღარ მიაღწევდა, მაგრამ ასე არ მომხდარა, ანუ ფარული ცვლადები არ არსებობს
ექსპერიმენტები ბელის უტოლობაზე
ჯონ კლაუზერმა კალციუმის ატომები გამოიყენა, რომელთა სპეციალურად განათების გზითაც გადაჯაჭვული ფოტონები გაუშვა. მან ფილტრები ორივე მხარეს დააყენა, რათა ფოტონების პოლარიზაცია გაეზომა და დაამტკიცა, რომ შედეგებმა ბელის უტოლობა დაარღვია.

ფოტო: The Nobel Prize
ალენ ასპემ ახალი მეთოდი შეიმუშავა, რომლის მეშვეობითაც ფოტონები უფრო სწრაფად გაუშვა. ასევე, პარამეტრებს ცვლიდა, რათა სისტემაში ზედმეტი ინფორმაცია არ მოხვედრილიყო, რომელიც შედეგზე იქონიებდა გავლენას.
ფოტო: The Nobel Prize
ანტონ ცაილინგერმა გადაჯაჭვული ფოტონების წყვილი შექმნა, რაც კრისტალზე ლაზერის მინათებით მოახერხა. მან გაზომვითი პარამეტრების ცვლილებისთვის შემთხვევითი რიცხვები გამოიყენა. ფიზიკოსმა ერთ-ერთ ექსპერიმენტში შორეული გალაქტიკებიდან წამოსული სიგნალებით ფილტრები გააკონტროლა ისე, რომ სიგნალები ერთმანეთზე არ ზემოქმედებდა.
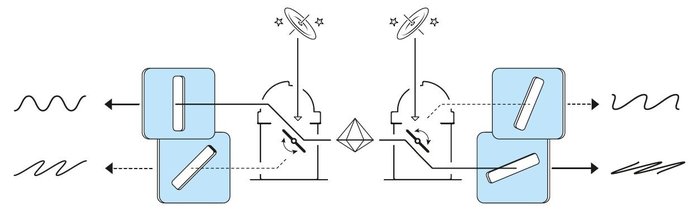
ფოტო: The Nobel Prize
ჩამოთვლილმა ექსპერიმენტებმა კვანტური ინფორმაციის შემსწავლელი მეცნიერების განვითარებასა და ამ მხრივ ახალი ერის დასაწყისს დაუდო საფუძველი, რადგან კვანტური მდგომარეობებით მანიპულაცია უდიდესი პოტენციალის მქონე ტექნოლოგიების შექმნის წინაპირობაა.











კომენტარები