როგორ ვასწავლოთ მათემატიკა საკუთარ თავს

ფოტო: Klara Kim
ჩემმა ფიზიკის მასწავლებელმა, ილია ლომიძემ ერთხელ მითხრა, რომ ფიზიკა მათემატიკის გარეშე უბრალოდ საბავშვო ზღაპარია. იმის გამო, რომ სკოლის ბოლო წლებში ფიზიკაზე ჩაბარებას ვგეგმავდი, მასწავლებლის სიტყვები ისეთი სიმართლე იყო, რომელიც აუცილებლად უნდა გამეგო. სკოლის პერიოდში IYPT-ში (International Young Physicists tournament) ვმონაწილეობდი, რომელიც მოსწავლეებს ასე თუ ისე წარმოდგენას უქმნიდა იმის შესახებ თუ როგორია ფიზიკოსობა და როგორია თეორიული ფიზიკა.
კონკრუსის ფარგლებში მოსწავლეებს რამდენიმე ამოცანაზე უნდა ემუშავათ, ოღონდ ეს ამოცანები ძალიან ზოგადი იყო. მაგალითად, გამოიკვლიეთ პინგ-პონგის ბურთის ლევიტაცია ჰაერის მუდმივ ნაკადში. ექსპერიმენტი ასე გამოიყურებოდა და ის მოსწავლებს მეტწილად ბერნულის კანონის შესწავლის საშუალებას აძლევდა
რადგან მსგავსი ამოცანები მომწონდა, გადავწყვიტე მათემატიკას ცოტა სერიოზულად მოვკიდებოდი და იმაზე მეტი მესწავლა, ვიდრე სკოლაში მასწავლიდნენ. ისეთი წარმოდგენა მქონდა, რომ მათემატიკა ფიზიკისთვის უნდა მესწავლა. ანუ, ფიზიკოსი ვერ ვიქნებოდი მათემატიკა რომ არ მცოდნოდა და ამას არც ისე დიდი ხალისით ვაკეთებდი.
წლები გავიდა, ჩემი ინტერესები შეიცვალა და ნელ-ნელა აღმოვაჩინე, რომ მათემატიკა საერთოდ არ ვიცი. მეტიც, მათემატიკა მათაც არ იციან, ვინც მათემატიკას კარგად სწავლობდნენ. მხოლოდ მეორე-მესამე კურსზე მივხვდი, რომ მათემატიკა მხოლოდ ხელსაწყო არაა, რომელსაც რაღაცებისთვის "ვიყენებთ". მათემატიკა არც ენა არაა, რომლითაც რაღაც ბუნებრივ ფენომენებს "ვთარგმნით", ის ბევრად მეტია. ის რასაც სკოლაში და უნივერსიტეტში გვასწავლიან, იქნება ეს ალგებრა, გეომეტრია თუ კალკულუსი... უფრო სწორად ისეთი სახით, როგორც ამას გვასწავლიან, რეალურად ბუღალტერიაა — არც კი.
მიუხედავად იმისა, რომ მათემატიკა კარგად არასდროს ვიცოდი, მათემატიკოსებისადმი და ფიზიკოსებისადმი რაღაც ბუნდოვანი პატივისცემა მქონდა. ჩემსავით ალბათ ბევრი თქვენგანია. აინშტაინის სახელი ყველასთვის ცნობილია და რომ დასვათ კითხვა, ვინ იყვნენ მსოფლიოს ყველაზე დიდი გენიოსები, ხშირად ისეთ ადამიანების სახელებს მიიღებთ, რომლებიც მათემატიკასთან "ასოცირდებოდნენ". მე ვფიქრობ, რომ ყველა ჩვენგანმა ვინც უბრალოდ ვინტერესდებით რაღაცებით და მეცნიერება, სამეცნიერო პროცესი მოგვწონს, მათემატიკა ხელახლა უნდა ვისწავლოთ. ოღონდ მართლა ვისწავლოთ. ეს ერთ-ერთი მიზანია, რომელიც წელს დავისახე.
მათემატიკა ყველაზე "წმინდა" ფილოსოფიაა
ფოტო: Domain of Science
ერთ-ერთი რამ, რაც ჩვენ მათემატიკურ ცოდნას ძალიან აკლია, მათემატიკის ფილოსოფია და ისტორიაა. როცა რაღაც პოლიტიკური მოვლენა ხდება, მაგალითად 2008 წლის აგვისტოს ომი აიღეთ, საომარი პროცესების გარდა, მთავარ ინტერესს მის მიღმა არსებული პოლიტიკური პროცესებით ვინტერესდებით. როგორ მივედით აქამდე? შეიძლებოდა თუ არა ამის არიდება?
როცა პიროვნებისადმი რომანტიულად ხართ განწყობილი, ხშირად მისი წარსულით ინტერესდებით, მისი "ბნელი" და "ნათელი" მოდელებით, რათა ადამიანზე წარმოდგენა შეგექმნათ. იგივენაირად, როცა გენეტიკით ინტერედებით, სწავლას მენდელით იწყებთ, შემდეგ მორგანს სწავლობთ, მერე დნმ-ის სხვადასხვა მოდელებს და ა.შ.
რაღაც ცნება, იქნება ეს ომი, სიყვარული, გენეტიკა თუ ტრიგონომეტრია... უფრო გასაგები მაშინაა, როცა ვხედავთ როგორ მივიდა საქმე აქამდე. სკოლაში და უნივერსიტეტშ მათემატიკური მიგნებების ისტორიულ კონტექსტს და მის მიღმა არსებულ ნააზრევს ნაკლებად ვსწავლობთ და რაც მთავარია ნაკლებად ვფიქრობთ.
მაგალითად, ძალიან ნათლად მახსოვს როგორ მასწავლიდნენ კომპლექსურ რიცხვებს. რა არის კომპლექსური რიცხვი? პასუხი მარტივია: ნამდვილი და წარმოსახვითი რიცხვის ჯამი. ყველაზე ცნობილი წარმოსახვითი რიცხვი √-1-ია, ანუ i. π კომპლექსური რიცხვია და ა.შ. მაგრამ რატომ?
უფრო სწორად რა საჭიროა ეს რიცხვები? მათემატიკაში, ისევე როგორც მეცნიერებაში, მკვლევრებს გარკვეული ცნებები საჭიროების მიხედვით შემოაქვთ. იმისთვის, რომ მათემატიკური ცნებების არსი გვესმოდეს, მხოლოდ არითმეტიკული სამუშაოების შესრულება საკმარისი არაა. კომპლექსურ და წარმოსახვით რიცხვებზე უამრავი წიგნი დაწერილა, თუმცა ერთ-ერთი საუკეთესო, რომელიც "არა-მათემატიკოსებისთვისაც" გასაგებია, პოლ ჯ. ნაჰინის წიგნი "An Imaginary Tale" არის. დაახლოებით 250 გვერდიანი წიგნი, რომელიც მხოლოდ √-1-ს ეხება.
თუ სადღაც გულის სიღრმეში ცნობისმოყვარეობა გჭამთ და გსურთ მათემატიკას სხვა კუთხით შეხედოთ, ეს წიგნი შესანიშნავი დასაწყისია. თუმცა, იმისთვის რომ ეს წიგნი "გაიგოთ", სკოლის მათემატიკა, ცოტა ტრიგონომეტრია უნდა გახსოვდეთ. თუ არ გახსოვთ, მაშინ შეგიძლიათ გაიხსენოთ და ცნობისმოყვარეობის დასაკმაყოფილებლად ინტერნეტი მოქექოთ.
მათემატიკა, სხვა ნებისმიერი ფილოსოფიური დისციპლინის მსგავსად, მონდომებას საჭიროებს. ანუ, წიგნს უბრალოდ კი არ უნდა კითხულობდეთ, მას უნდა იკვლევდეთ.
ფილოსოფია მხოლოდ ეგზისტენციური საკითხების განხილვა არაა. სამწუხარო რეალობაა, მაგრამ ფაქტია, რომ გარკვეული ადამიანები ვინც მეცნიერების პოპულარიზაციით კავდებიან, ფილოსოფიას უგულებელყოფენ. თითქოს, ფილოსოფია მხოლოდ ისეთ საკითხებს ეხება, როგორიცაა "რა არის მნიშვნელობის მნიშვნელობა", როგორც ამას ნილ დეგრას ტაისონი აღნიშნავს. ეს ტყუილია. თუ კი სადმე ფილოსოფია საჭიროა, ეს მათემატიკაშია.
2+2=4? რატომ?
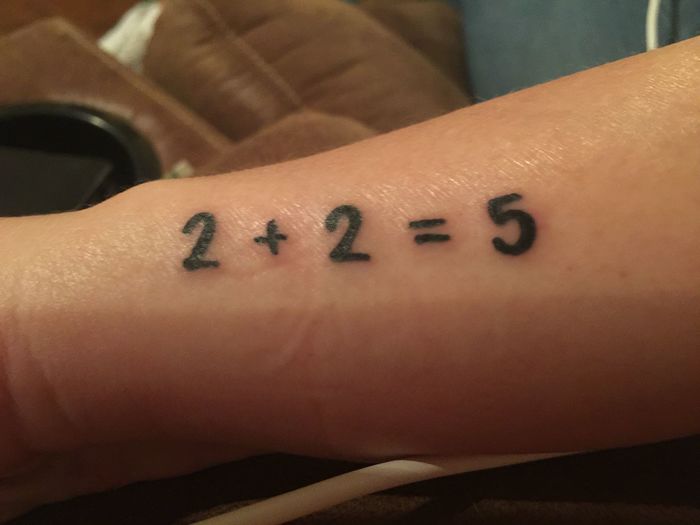
მეოცე საუკუნეში უცნაური ფილსოოფიური მიმდინარეობა აღმოცენდა — ლოგიკური ატომიზმი. მისი მიმდევრების მტკიცებით, ფილოსოფოსები ხშირად "უაზრო" საკითხებს განიხილავენ. მაგალითად, ფილოსფოსი, რომელიც სვამს კითხვას "რა არის სიყვარული", უბრალოდ დროს ხარჯავს. პოზიტივისტებმა, ფილოსოფოსი ლუდვიგ ვიტგენშტაინის და ბერტრან რასელის გავლენით, გადაწყვიტეს, რომ ფილოსოფია "გაეწმინდათ".
მათი მტკიცებით, ლოგიკური ტავტოლოგიები ჭეშმარიტების ყველაზე ელემენტარული "ატომები" იყო. ერთგვარი საშენი ბლოკები მთელი მეცნიერებისთვის. ავიღოთ ასეთი ლოგიკური წინადადება "a=y" ან "a≠y", "ბურთი ან მწვანეა ან ბურთი არაა მწვანე". რა ფერისაც არ უნდა იყოს ბურთი, ეს წინადადება მართალი იქნება. ეს ჭეშმარიტების ყველაზე "ელემენტარული" ფორმაა და აქედან უამრავი რამ გამომდინარეობს. მაგალითად, თუ A>B>C-ზე, მაშინ A>C და ა.შ.
ლოგიკური ატომიზმის მიხედვით, ტავტოლოგია a priori ცოდნას ასახავს, ანუ ცოდნას, რომელსაც გამოცდილებით კი არ ვიღებთ, არამედ ამ ცოდნით ასე ვთქვათ "ვიბადებით". ამ აპრიორული ცოდნიდან დედუქციით და ლოგიკური აზროვნებით შეგვიძლია სხვა, უფრო "რთულ ჭეშმარიტებებამდე" მივიდეთ.
ლოგიკური ატომიზმის მიმდევართა მტკიცებით, მათემატიკა მთლიანად აპრიორული ცოდნაა. შესაბამისად, ისეთი მარტივი რამ, როგორიც მიმატებაა, არც ისე მარტივია, რადგან მათემატიკური ოპერაციების ემპირიულად გამართლება არასწორია. 1 ფორთოხალს რომ 1 ფორთოხალი დავუმატოთ, შედგად 2 ფორთოხალს მივიღებთ, დამაკმაყოფილებელი აღარაა, რადგან შეკრების მხოლოდ "ემპირიული" გამართლება არ გვაწყობს. ნებისმიერი მათემატიკური ოპერაცია ლოგიკიდან უნდა გამომდინარეობდეს, თან ყველაფერი ძალიან ზუსტად უნდა იყოს განმარტებული, რათა ბუნდოვანების ადგილი არ დარჩეს.
სწორედ ამიტომ, რასელს და ვაითჰედს თავიანთ რევოლუციურ წიგნში 379 გვერდი დასჭირდათ იმის დასამტკიცებლად (ლოგიკურად), რომ 1+1=2-ს.
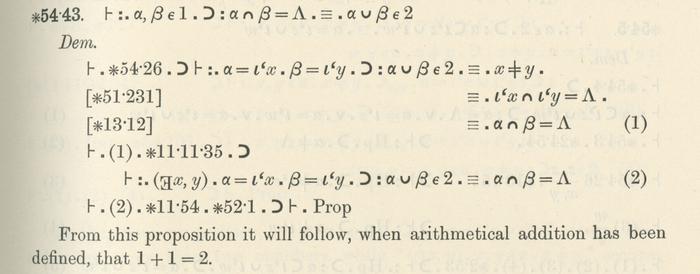
ფოტო: Public Domain
ლოგიკურ ატომიზმს, როგორც ფილოსოფიურ მოძრაობას სერიოზული პრობლემები შეექმნა, მას შემდეგ, რაც კურტ გოდელმა მათემატიკის ფილოსოფია სამუდამოდ შეცვალა, თუმცა გარკვეული კითხვები დღემდე პასუხგაუცემელია. ზოგი მათემატიკოსი მიიჩნევს, რომ რიცხვები და მათემატიკა, ისევე როგორც სხვა ცნებები უბრალოდ, ჩვენ გონებაშია და ის რეალობას არ აღწერს. მაგალითად, ჩვენ გონებაში გვაქვს "მთის ცნება", თუმცა გერმანიაში, ნაკლებად მთიან ადგილში, მთად ხშირად ისეთ შემაღლებებს მოიხსენიებენ, რასაც ჩვენ საქართველოში გორას ვეძახით.
გორა და მთა ორი მსგავსი, მაგრამ განსხვავებული ცნებებია. როდის წყვეტს გორა გორობას და როდის ხდება ის მთა? "მთის" და "გორის" ცნებები, ისევე როგორც უამრავი სამეცნიერო ტერმინი, უბრალოდ პირობითია. გარკვეული ცნების განმარტება კონტექსტის მიხედვით იცვლება, შეგვიძლია თუ არა იგივე ვთქვათ მათემატიკაზე?
მათემატიკოსები მათემატიკის საფუძველზე ვერ თანმხდებიან და ამ გაგებით, მათემატიკა არც ისე "ზუსტი მეცნიერებაა". ამ საკითხზე, ისევე როგორც მათემატიკაში არსებულ ზოგად ფილოსოფიურ პრობლემებზე შესანიშნავი წიგნი დაწერა მორის კლაინმა, სახელწოდებით "The Loss of Certainty", რომელიც უკეთეს წარმოდგენას შეგიქმნით იმის შესახებ თუ რა არის მათემატიკა.
"თოფურია" იყო და არის საუკეთესო წიგნი

ფოტო: Public Domain
70-იანებში დაბეჭდილი "მათემატიკა", თოფურიას, ხოჭოლავას და სხვების მიერ, დღემდე ერთ-ერთი საუკეთესო სასკოლო სახელმძღვანელოა, რაც კი ქართულ ენაზე დაწერილა. გასაოცარი კი ისაა, რომ დროთა განმავლობაში ის კიდევ უკეთესი გახდა მათემატიკის სწავლისთვის. ყველაზე შთამბეჭდავები ამოცანები კი არა, თოფურიას წიგნის "თეორიული" ნაწილია, სადაც საოცარი ლაკონურობით, მაგრამ გასაგებად არის შეჯამებული მთელი სასკოლო მათემატიკა.
სკოლაში ამ წიგნით სწავლა დიდად კარგი არ არის. სხვა უფრო თანამედროვე სახელმძღვანელოები, განსაკუთრებით ინგლისურენოვანი წიგნები უფრო მარტივად და ვრცლად აღწერს ძალიან საჭირო ცნებებს. თუმცა, თოფურიას წიგნის კითხვა და ამოცანების კეთება, მათემატიკის უფრო ფილოსოფიური ნაწილის სწავლასთან ერთად ძალიან სასარგებლოა. თუ ახლა გეგმავთ, რომ საკუთარ თავს მათემატიკა ასწავლოთ, სკოლა, ალბათ, უკვე დამთავრებული გაქვთ და ის შიში არ გაქვთ, რომ მასწავლებელი გამოცდაში ჩაგჭრით, ან დავალებაში ორიანს მიიღებთ.
ამოცანების კეთება მნიშვნელოვანია, რათა ზოგადად საგანს ალღო აუღოთ და ერთგვარი ინტუიცია გამოიმუშაოთ. ამისთვის სასკოლო და საუნივერსიტეტო სახელმძღვანელოები გამოგადგებათ. დასაწყისისთვის შესანიშნავი წიგნია, სუზანა ს. ეპის Discrete Mathematics with Applications.
მათემატიკის სწავლას სერიოზულად თუ მოეკიდებით აღმოაჩენთ, რომ ყველა მეცნიერება, ბიოლოგიიდან დაწყებული, ფიზიკით და კომპიუტერული მეცნიერებით დამთავრებული, ბევრად გასაგებია, რადგან საბოლოო ჯამში, ნებისმიერი საბუნებისმეტყველო მეცნიერება კანონზომიერებებს სწავლობს.
მათემატიკის სწავლა ინტელექტუალური სიამოვნების უშრეტი წყაროა. მე პირადად, იმდენად მოვიხიბლე პერსპექტივით, რომ "ზოგადი მათემატიკური" წიგნების კითხვის გარდა, უბრალოდ სასკოლო ალგებრას და ტრიგონომეტრიას მივუბრუნდი. ახლაც მახსენდება ჩემი ფიზიკის მასწავლებლის სიტყვები, რომ ფიზიკა მათემატიკის გარეშე უბრალოდ ზღაპარია. მეტსაც ვიტყოდი, მეცნიერება მათემატიკის გარეშე ზღაპარია და მათემატიკა, ფილოსოფიის გარეშე უბრალოდ ბუღალტერიაა.












კომენტარები