ბაბილონის ბიბლიოთეკა: წიგნები, რომლებშიც თქვენზე ყველაფერი წერია

წარმოიდგინეთ ბიბლიოთეკა, რომელში არსებული წიგნებიც ასოების ყველა იმ კომბინაციას შეიცავს, რაც ოდესმე დაწერილა, ან შეიძლება რომ დაიწეროს.
თუ ამაზე დაფიქრდებით, მიხვდებით, რომ ეს იდეა წარმოუდგენლად უცნაურია. ასოების ყველა კომბინაციის არსებობა ნიშნავს, რომ ბიბლიოთეკაში ყველა წიგნია, რომელიც ოდესმე დაწერილა, ან შეიძლება დაწერილიყო. ასეთ წიგნებში დაგვხვდებოდა ყველა სამეცნიერო გადატრიალება, ყველა სიყვარულის ისტორია, ხელოვნების ნიმუში, ადამიანები, რომელთა შესახებაც არასდროს გვსმენია, ნებისმიერი ამბავი, რაც ოდესმე მომხდარა ან მოხდება. მათში ყველა ჩვენგანის დაბადებისა და სიკვდილის ზუსტ ამბავსაც ამოიკითხავთ.
ასეთი ბიბლიოთეკის შესაქმნელად თითქმის უსასრულო რაოდენობის ქაღალდი, მელანი და დრო დაგჭირდებოდათ, თუმცა სანამ აქამდე მივალთ, ცოტა ამ ბიბლიოთეკის სულის ჩამდგმელზეც ვისაუბროთ.
ხორხე ლუის ბორხესი
ხორხე ლუის ბორხესი არგენტინელი მწერალი და პოეტი იყო, ის მე-20 საუკუნის ლიტერატურული სამყაროს ერთ-ერთი ყველაზე გამორჩეული ფიგურად ითვლება. არგენტენელი ავტორის მოკლე მოთხრობა ბაბილონის ბიბლიოთეკა პირველად 1941 წელს მისი მოთხრობების კრებულში დაიბეჭდა. სწორედ ამ მოთხრობაში აღგვიწერს ის ჰიპოთეტურ ბიბლიოთეკას.

ფოტო: Public Commons
წიგნში ავტორი მოგვითხრობს სამყაროზე, რომელიც წარმოუდგენელი რაოდენობის ერთმანეთის თავზე განლაგებული ექვსკუთხედის ფორმის ოთახებისგან შედგება. თითოეულ ოთახში ოთხ კედელზე არსებული წიგნებით სავსე თაროები და ის მინიმალური პირობებია, რაც ადამიანს გადარჩენისთვის სჭირდება.
მიუხედავად იმისა, რომ წიგნების განლაგება შემთხვევითია და მათში არსებული ტექსტებიც შემთხვევით დაწყობილი ასოების კომბინაციებია, მის მაცხოვრებლებს მიაჩნიათ, რომ ეს წიგნები ასოების ყველა შესაძლო კომბინაციას მოიცავს, შეაბამისად ეს ბიბლიოთეკა ყველა სისულელესთან ერთად ასევე უნდა შეიცავდეს ყველა იმ წიგნს, რაც ოდესმე დაწერილა, ან დაიწერება და მათ ყველა შესაძლო ცდომილ ვარიანტს.
ბიბლიოთეკის წარმოუდგენელი ზომის გამო, ისინი წიგნების უმეტესობაში ვერც წინადადებებს და ვერც სიტყვებს ვერ პოულობენ, ბიბლიოთეკა პრაქტიკულად გამოუსადეგარია, ამას კი იქ მცხოვრებნი ფსიქიკურ აშლილობამდე მიჰყავს.
იდეის რეალობად ქცევა
ციფრული სამყაროს განვითარებამდე მსგავსი ბიბლიოთეკა მხოლოდ და მხოლოდ ფანტასტიკის სფერო იყო. ჯონათან ბასილი კოლუმბიის უნივერსიტეტის ინგლისური ლიტერატურის ფაკულტეტზე სწავლობდა, როდესაც ბაბელის ბიბლიოთეკის შესახებ გაიგო. მან გაიაზრა, რომ მისი შექმნა კომპიუტერების დახმარებით შესაძლებელი იქნებოდა, ამიტომაც გადაწყვიტა, ბორხესის იდეა სისრულეში მოეყვანა.
თავდაპირველად მან ტრადიციული მიდგომები სცადა და აღმოაჩინა, რომ ასეთი სიდიდის ბიბლიოთეკის ციფრულ ფორმატში შენახვა მისი უზარმაზარი ზომის გამო ფიზიკურად შეუძლებელი იყო. თუმცა მან ჭკვიანური გამოსავალი მოიფიქრა და შექმნა ბიბლიოთეკა, რომელიც ალგორითმის სახით არსებობს. ჯონათანის ციფრული ბიბლიოთეკა ბორხესის ორიგინალი ნაწარმოების მსგავსად ექვსკუთხედის ფორმის ოთახებისგან შედგება, ოთახში ოთხი კარადაა, თითოეულზე ექვსი თაროა, რომელზეც 32 წიგნი დევს, თითოში კი 410 გვერდია.
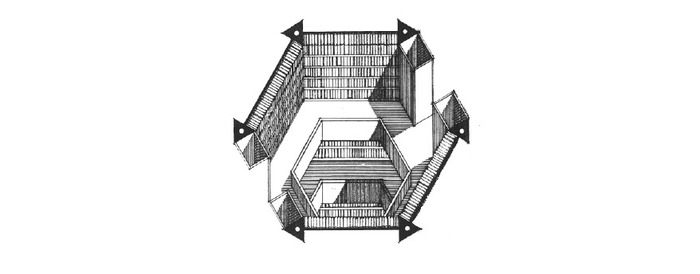
ციფრული ბიბლიოთეკის ექვსკუთხა ოთახი.
ფოტო: REPRODUÇÃO
როგორ მუშაობს ბაბილონის ციფრული ბიბლიოთეკა?
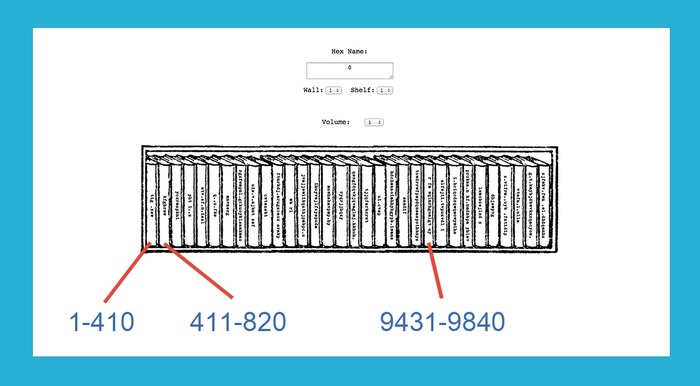
თითოეულ წიგნში თითოეულ გვერდს უნიკალური რიცხვი აქვს მინიჭებული, მაგალითად, პირველი ოთახის პირველი კარადის პირველ თაროზე არსებული პირველი წიგნის ბოლო გვერდი 410-ეა, ხოლო მისი შემდეგი, ანუ მეორე წიგნის პირველი გვერდი კი 411-ე.
გვერდებზე მოცემულ ტექსტს კი თავად გვერდის ნომერი განსაზღვრავს. ჯონათანის მიერ შექმნილი ალგორითმი გვერდის ნომერს მისივე (გვერდის) შინაარსის გენერირებისთვის იყენებს. მაგალითად, რომ ვნახოთ თუ რა წერია გვერდ 451-ზე, ჩვენ ეს ნომერი ალგორითმში უნდა შევიყვანოთ, ის კი მათემატიკური გარდაქმნების საშუალებით მისგან ტექსტს შექმნის.
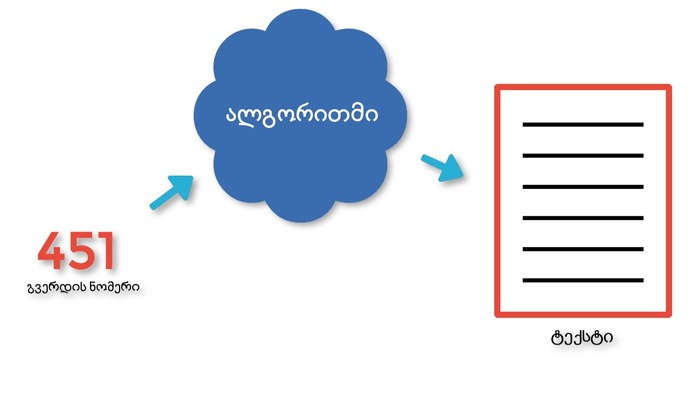
ჯონათანმა ალგორითმი ისე შეიმუშავა, რომ მან ასოების ყველა შესაძლო კომბინაცია მოგვცეს. ხოლო ალგორითმში ერთი და იგივე რიცხვის შეყვანა ყოველ ჯერზე ერთი და იგივე შედეგს გვაძლევს. ეს ნიშნავს, რომ ალგორითმი გვერდ 451-ის აკრეფვისას, ყოველთვის იდენტურ ტექტს შექმნის.
რას ნიშნავს ეს ყველაფერი?
ეს ნიშნავს იმას, რომ ნებისმიერ გვერდზე არსებული ტექსტი წინასწარვეა განსაზღვრული, ანუ ბიბლიოთეკაში არსებული ყველა წიგნის ყველა გვერდი, რაღაც გაგებით, უკვე არსებობს. ტექსტები გვერდის ნომერშივეა დაშიფრული.
ამ ამბავში ყველაზე მნიშვნელოვანი ის ფაქტია, რომ ალგორითმი უკუღმაც მუშაობს. ჩვენ შეგვიძლია მას ნებისმიერი ტექსტი მივცეთ, ის კი ტექსტს გვერდის ნომრად გადათარგმნის და ბიბლიოთეკაში გვიპოვნის ოთახს, კარადას, თაროს, წიგნს და გვერდს, რომელზეც ეს ტექსტი გვხვდება.
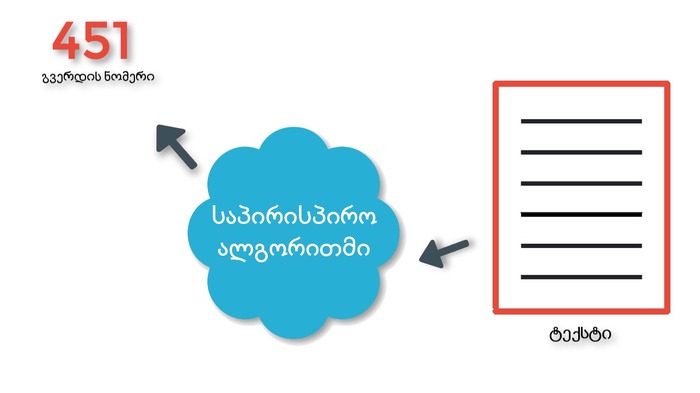
ეს ყველაფერი ძალიან უცნაურია
ნამდვილად. თქვენ საიტზე შეგიძლიათ ნებისმიერი ტექსტი შეიყვანოთ, ალგორითმი კი გიპოვნით, თუ რომელი წიგნის რომელ გვერდზე წერია ის. მოდი The Beatles-ის ცნობილი სიმღერა მოვძებნოთ და ვნახოთ, არის თუ არა ის ბიბლიოთეკაში.
რა თქმა უნდა არის. Yesterday-ს ტექსტი ერთ-ერთი ექვსკუთხედის, პირველი კარადის მესამე თაროს პირველი წიგნის 364 გვერდზეა. განსაცვიფრებელი ფაქტი ის არის, რომ ეს ტექსტი აქ მანამდეც იყო, სანამ მას პოლ მაკარტნი დაწერდა. თქვენ თავად შეგიძლიათ შეხვიდეთ საიტზე და მოძებნოთ ნებისმიერი რამ: ვეფხისტყაოსანი, რაიმე მათემატიკური ფორმულა, სიზმარი, რომელიც გუშინ დაგესიზმრათ, ესსე, რომელიც ერთიან ეროვნულ გამოცდებზე დაწერეთ, თქვენი ბოლო დაბადების დღის ზუსტი აღწერა, ეს სტატია. ალბათ ხვდებით, რომ სია უსასრულოა.
გამოგონება თუ აღმოჩენა?
ეს ბიბლიოთეკა განსხვავებას აღმოჩენასა და გამოგონებას შორის ბუნდოვანს ხდის. თუ თქვენ ანტიგრავიტაციულ მოწყობილობას გამოიგონებთ, არის ეს თუ არა ნამდვილი გამოგონება, თუ გავითვალისწინებთ იმ ფაქტს, რომ მისი ზუსტი აღწერა ამ ბიბლიოთეკაში უკვე სადღაც წერია?
წერია ისევე, როგორც თერმოდინამიკის ყველა კანონი, ზოგადი ფარდობითობის თეორია, ჩარლზ დარვინის ყველა ნაშრომი და ა.შ.
ბაბელის ბიბლიოთეკაში 10 ხარისხად 5000 გვერდია, შესადარებლად, ხილულ სამყაროში ატომების რაოდენობა მხოლოდ 10 ხარისხად 80-ია.
თუ ყველაფერი უკვე სადღაც წერია, კარგავს თუ არა აზრს ყველაფერი?
ალბათ სწორი იქნება თუ ვიფიქრებთ, რომ კომპიუტერული პროგრამის მიერ გაუცნობიერებლად შედგენილ ტექსტსა და ადამიანის გამიზნულ ნათქვამს შორის განსხვავება არსებობს. ჩვენ კომუნიკაციისთვის სასრული რაოდენობის სიმბოლოებს ვიყენებთ, რის გამოც შესაძლებელია შეიქმნას ისეთი ბიბლიოთეკა, რომელშიც ამ სიმბოლოების ყველა შესაძლო კომბინაციას, შესაბამისად ყველა შესაძლო სიტყვასა და წინადადებას შეიცავს. მაგრამ, მხოლოდ ის ფაქტი, რომ ეს ყველაფერი სადღაც წერია არ ნიშნავს, რომ ეს ყველაფერი უკვე ნათქვამია.
ალბათ ჯობია ვიკითხოთ, ყველა იმ შესაძლო წინადადებებიდან, რაც შეიძლება სასრული ასოების კომბინაციით შედგეს, რომელი წინადადება იქნება, რომლის პირველად თქმასაც ჩვენ შევძლებთ?














კომენტარები