დინამიკური პროგრამირება ერთ-ერთი ფართოდ გამოყენებადი და ძალიან მნიშვნელოვანი ალგორითმული პარადიგმაა, რომელსაც ოპტიმიზაციის ამოცანების ამოხსნაში განსაკუთრებული როლი უჭირავს და გვეხმარება გავაუმჯობესოთ ალგორითმის მუშაობის დრო. წარსულში რომ გავიხედოთ, მისი შექმნის ამბავი ჯერ კიდევ გასული საუკუნის 50-იანი წლებიდან იწყება.

1950 წელს დინამიკურ პროგრამირებას საფუძველი ჩაუყარა ამერიკელმა მათემატიკოსმა რიჩარდ ბელმანმა. პარადიგმის სახელში გამოყენებული სიტყვა "პროგრამირება" ნაკლებადაა კავშირში ამ სიტყვის თანამედროვე გაგებასთან და კომპიუტერული კოდის შექმნასთან. ის უფრო მათემატიკური მეთოდია ოპტიმიზაციის ამოცანების ამოსახსნელად. მისთვის ამ სახელის დარქმევას კი საინტერესო ისტორია აქვს.

როგორც რიჩარდ ბელმანი საკუთარ ავტობიოგრაფიაში აღწერს, 1950 წლის შემოდგომა მან RAND-ში გაატარა. ეს იყო კორპორაცია, რომელიც ამერიკის საჰაერო თავდაცვას ემსახურებოდა. ამ უკანასკნელს კი მაშინდელი თავდაცვის მდივანი, უილსონი ხელმძღვანელობდა, რომელსაც, ბელმანის თქმით, სიტყვების — "მათემატიკა" და "კვლევა" პათოლოგიური შიში ჰქონდა.

"მისი სახე ივსებოდა, წითლდებოდა და შესაძლოა დანაშაულიც კი ჩაედინა, თუ ვინმე მის სიახლოვეს ამ სიტყვებს [მათემატიკასა და კვლევას] ახსენებდა", — აღნიშნავს ბელმანი.

ამიტომ ბელმანმა იგრძნო, რომ მისი აღმოჩენისთვის ისეთი სახელი უნდა მოეფიქრებინა, რომელიც მის ნაშრომს უილსონისგან დაიცავდა და არ გამოააშკარავებდა იმ ფაქტს, რომ ბელმანი RAND Corporation-ში მათემატიკაში კვლევებით იყო დაკავებული. საბოლოოდ მისთვის "დინამიკური პროგრამირების" დარქმევა გადაწყვიტა, რომელიც ცხადად მათემატიკასთან არ ასოცირდება. ამ კონტექსტში სიტყვა "პროგრამირება" უნდა გავიგოთ როგორც "დაგეგმარება", ხოლო რას შეიძლება გამოხატავდეს "დინამიკური", ამაზე ცოტა მოგვიანებით, როცა პარადიგმას უკეთ გავეცნობით.

დინამიკური პროგრამირება ამოცანის ამოსახსნელად იყენებს მისი ქვეამოცანების გადაფარვის თვისებას. ეს ქვეამოცანები (იგივე ამოცანა, თუმცა ნაკლები მონაცემისთვის) კი წარმოიშობა რეკურსიული კავშირით მოცემული ამოცანის ამონახსნსა და მისი ქვეამოცანების ამონახსნს შორის. ანუ მათი ოპტიმალური ამონახსნი უნდა გვეხმარებოდეს მთლიანი ამოცანის ოპტიმალური ამონახსნის პოვნაში.

უმეტესად, დინამიკური პროგრამირება ოპტიმიზაციის ამოცანების ამოსახსნელად გამოიყენება. ხშირ შემთხვევაში ჩვენ შეგვიძლია ამოცანა დინამიკური პროგრამირების გარეშეც ამოვხსნათ, თუმცა მისი მეშვეობით ამონახსნის პოვნა და ოპტიმიზაცია გაცილებით ეფექტური და მოსახერხებელია. ოპტიმიზაციის ამოცანებს შესაძლოა არაერთი დასაშვები ამონახსნი ჰქონდეს. თითოეულ მათგანს რაღაც მნიშვნელობა (value) შეესაბამება და ჩვენი მიზანია ოპტიმალური მნიშვნელობის მქონე ამონახსნის პოვნა, ანუ ამონახსნის ისე შერჩევა, რომ მისი მიზნის ფუნქციაში (ფუნქცია, რომელიც ჩვენს ინტერესს აღწერს) ჩასმისას მივიღოთ მაქსიმალური ან მინიმალური (დამოკიდებულია ამოცანაზე) მნიშვნელობა.

დინამიკური პროგრამირება ამოცანას ჰყოფს ქვეამოცანებად და მათი ამონახსნებისგან ვიღებთ თავდაპირველი ამოცანის ამონახსნს.

თუმცა მაინც რა არის ქვეამოცანა?

ვთქვათ, გვინდა ვიპოვოთ x-ს ფაქტორიალი. ამ ამოცანის ქვეამოცანად შეგვიძლია (x-1)-ს ფაქტორიალის პოვნა განვიხილოთ. თუ გვეცოდინება (x-1)-ს ფაქტორიალი, მისი x-ზე გამრავლებით მოცემული ამოცანის ამონახსნსაც ვიპოვნით, თუმცა თავის მხრივ (x-1)-ს ფაქტორიალის პოვნაც იშლება ქვეამოცანებად, როგორიცაა (x-2)-ის ფაქტორიალის პოვნა, შემდეგ კი მის საპოვნელად საჭირო (x-3)-ის ფაქტორიალის პოვნა და ა.შ.

დინამიკური პროგრამირების პარადიგმაში მნიშვნელოვანია, რომ ქვეამოცანები ამოიხსნება მხოლოდ ერთხელ და შეინახება რაიმე მონაცემთა სტრუქტურაში. ასე რომ, თუ ქვეამოცანის ამონახსნი კიდევ დაგვჭირდება, ჩვენ არ მოგვიწევს მისი ხელმეორედ გამოთვლა და გამოვიყენებთ ერთხელ უკვე მიღებულ და დამახსოვრებულ შედეგს.

მაგალითად, წარმოიდგინეთ გაქვთ ფანქრების ყუთი და უნდა დაითვალოთ მასში არსებული ფანქრების რაოდენობა. როცა მის დათვლას მორჩებით, გაძლევენ კიდევ ერთ ფანქრებიან ყუთს და გთხოვენ დაითვალოთ ფანქრების ჯამური რაოდენობა ორივე ყუთში. რა თქმა უნდა, თქვენ არ დაიწყებთ პირველ ყუთში არსებული ფანქრების თავიდან დათვლას, არამედ დაითვლით ფანქრების რაოდენობას მხოლოდ მეორე ყუთში და დაუმატებთ მას პირველ ყუთში მოთავსებული ფანქრების უკვე დათვლილ და დამახსოვრებულ რაოდენობას. ასე შეგვიძლია წარმოვიდგინოთ დინამიკური პროგრამირების ძირითადი იდეა. ამგვარად, მის უპირატესობად შეგვიძლია ჩავთვალოთ ამოცანის ამოხსნის სისწრაფე, თუმცა არ უნდა დაგვავიწყდეს უარყოფითი მხარეც, რაც არის მეხსიერების პრობლემა, რომელსაც ვიყენებთ ქვეამოცანების ამონახსნების შესანახად და ძირითად შემთხვევაში, რაც უფრო დიდია საწყისი მონაცემები (input), მით უფრო მეტია ქვეამოცანების რაოდენობა და საჭირო მეხსიერებაც.

ახლა კი კონკრეტულ მაგალითებზე დაყრდნობით უფრო დეტალურად განვიხილოთ აღნიშნული ალგორითმული პარადიგმის გამოყენება და მნიშვნელობა.

დინამიკური პროგრამირება ფიბონაჩის მიმდევრობისთვის

ფიბონაჩის მიმდევრობის პირველი და მეორე წევრი ნულის და ერთის ტოლია, ხოლო ყოველი მომდევნო, წინა ორი წევრის ჯამს უდრის: F₁=0, F₂=1, F_n= F_(n-1) + F_(n-2)

ანუ მიმდევრობას ექნება შემდეგი სახე: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ....... განვიხილოთ ფიბონაჩის მიმდევრობის მე-n წევრის პოვნის ამოცანა:

ფორმულაზე დაყრდნობით დავწეროთ რეკურსიული ალგორითმი (როდესაც ფუნქცია საკუთარ თავს იძახებს), რომელიც უმარტივეს ლოგიკას ეყრდნობა: თუ n=1, ანუ ვეძებთ პირველ წევრს ალგორითმი დააბრუნებს 0-ს, ხოლო თუ n=2, მეორე წევრს - ანუ 1-ს. სხვა შემთხვევაში კი გამოიძახება იგივე ფუნქცია უფრო ნაკლები მონაცემებისთვის, ანუ ვპოულობთ და ვკრებთ მის წინა ორ წევრს:

თუმცა ზემოთ აღწერილი ალგორითმი ვერ ჩაითვლება დინამიკურ პროგრამირებად, რადგან ამ შემთხვევაში ჩვენ არ ვიმახსოვრებთ ქვეამოცანების ამონახსნებს, რაც გამოიწვევს ერთი და იგივე ქვეამოცანის რამდენჯერმე ამოხსნას, რაც დინამიკური პროგრამირების ფუნდამენტური იდეის დარღვევაა.

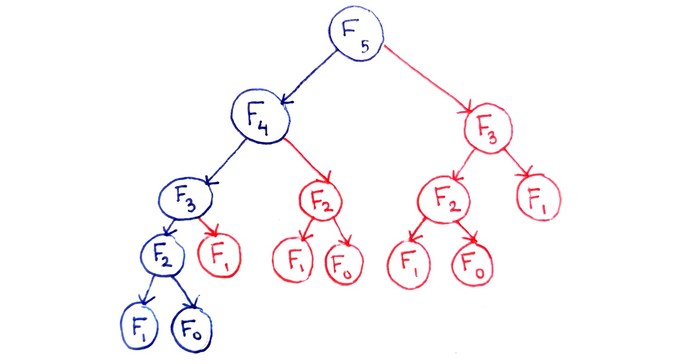
მოცემული სურათი აღწერს ალგორითმის მუშაობას, როდესაც ვეძებთ მიმდევრობის მე-5 წევრს. ყველა წრეში თითო ქვეამოცანაა, თუმცა წითლად ის ქვეამოცანებია შემოხაზული რომელიც ალგორითმს ერთხელ უკვე ამოხსნილი ექნებოდა, თუმცა ვინაიდან მისი შედეგი არ დაუმახსოვრებია, იძულებულია რამდენჯერაც დასჭირდება, ყოველ ჯერზე ხელთავიდან ამოხსნას. რაც უფრო გაიზრდება n (როცა ვეძებთ მიმდევრობის არა მე-5, არამედ 70-ე, მე-500, მე-1000 და ა.შ წევრს) ასეთი ქვეამოცანების რაოდენობაც გაცილებით მეტი იქნება, რაც ალგორითმის მუშაობის დროს მნიშვნელოვნად გაზრდის.

ამიტომ, ამ პრობლემის თავიდან ასარიდებლად, ვეცადოთ მისი დინამიკური პროგრამირების გამოყენებით გადაჭრას. ზოგადად, ვიდრე ალგორითმის შედგენაზე გადავიდოდეთ:

1. კარგად უნდა გავიაზროთ გამოგვადგება თუ არა მოცემული ამოცანისთვის დინამიკური პროგრამირების გამოყენება. გააჩნია თუ არა მას ქვეამოცანები და მიგვიყვანს თუ არა მათი ამონახსნები თავდაპირველი ამოცანის ამონახსნთან.
2. ამის შემდეგ საჭიროა ქვეამოცანების სტრუქტურის კარგად ჩამოყალიბება და დახასიათება. ჩვენი ამოცანის შემთხვევაში ქვეამოცანები მკაფიოდ იკვეთება, კერძოდ, ესენია: (n-1)-ე და (n-2)-ე წევრების პოვნა, რომელიც თავის მხრივ, მოითხოვს სხვა ქვეამოცანების ამოხსნას და (n-3), (n-4) ... (n-(n-3)) წევრების პოვნას. (n-2)-ე და (n-1)-ე წევრების პოვნის შედეგად კი, მათი შეკრებით პირდაპირ მივიღებთ ჩვენი ამოცანის პასუხს - მიმდევრობის მე-n წევრს.
3. ვაყალიბებთ რეკურსიულ კავშირს უფრო ფორმალურ ენაზე. ჩვენი ამოცანისთვის ეს შემდეგი ფორმულით გამოიხატება: F_n=F_(n-1)+F_(n-2)
4. განვსაზღვრავთ საბაზო შემთხვევას (საბაზისო ქვეამოცანას), რომელიც არის ქვეამოცანებს შორის ყველაზე მარტივი და მეტად აღარ დაიშლება. მაგალითად, როგორ ვიპოვნოთ ზედა საფეხურზე ჩამოყალიბებული რეკურსიული ფორმულით მიმდევრობის მეორე ან პირველი წევრი, რომელთაც „წინა ორი“ წევრი არ გააჩნიათ?! რა შევკრიბოთ?! ამიტომ, პირველი და მეორე წევრის პოვნა საბაზისო ქვეამოცანებია, რომლისთვისაც ამონახსნები პირდაპირ მოცემული გვაქვს (0 და 1). ხოლო n = 3 -დან დაწყებული ყველა წევრისთვის შესაძლებელია მოცემული ფორმულის გამოყენება.
5. და ბოლოს, ვირჩევთ დინამიკური პროგრამირების რომელი მიდგომა გამოვიყენოთ, ტაბულაცია თუ მემოიზაცია (რეკურსია). ფიბონაჩის მიმდევრობისთვის ორივე მათგანს გამოვიყენებთ, რაც გაგვიმარტივებს მათ შორის არსებული განსხვავების დანახვას.

იმისთვის, რომ პირველი ალგორითმი დინამიკური პროგრამირების პრინციპებზე გადავიყვანოთ საჭიროა მხოლოდ ერთი მასივის შემოტანა, რომელიც ქვეამოცანების ამონახსნებს შეინახავს. როდესაც ალგორითმი კონკრეტული ქვეამოცანის ამოხსნას "მიადგება", ვაკეთებთ შემოწმებას, არის თუ არა უკვე ჩვენს მასივში ამონახსნი ასეთი ქვეამოცანისთვის, თუ არის, პირდაპირ დავაბრუნებთ მას, წინააღმდეგ შემთხვევაში ალგორითმს ნებას ვრთავთ, ამოხსნას პირველად და სამომავლო გამოყენებისთვის შეინახოს ამონახსნი მასივში.

ალგორითმის ფსევდოკოდი:

ფსევდოკოდის პირველი სტრიქონი უზრუნველყოფს n-ელემენტიანი გლობალური მასივის შექმნას, რომელიც ავტომატურად ნულებით შეივსება. მეხუთე სტრიქონზე ვამოწმებთ - ისევ ნულის ტოლია თუ არა memo[n-1] (n-1 და არა n, რადგან მასივში ინდექსები 0-დან იწყება და მიმდევრობის პირველი წევრი, 0 ინდექსზეა, მეორე - 1-ზე, ხოლო მე-n წევრი n-1 -ზე იქნება). თუ ის ნულისგან განსხვავებულია ეს ნიშნავს, რომ ალგორითმს უკვე უპოვნია და მასივში შეუნახავს ის წევრი, რომელსაც ამჟამად ვეძებთ, ამიტომ პირდაპირ ვაბრუნებთ მას. წინააღმდეგ შემთხვევაში, ჩვეულებრივ, რეკურსიულ ფორმულაზე დაყრდნობით ვასრულებთ გამოთვლას და ამონახსნს მასივში ვინახავთ (როგორც უკვე აღვნიშნეთ, მე-n წევრის მისამართი მასივში n-1 ინდექსია). საბოლოოდ კი უნდა დავაბრუნოთ მე-n წევრი, ანუ memo[n-1].

წინა მეთოდში გამოყენებული რეკურსიის ნაცვლად, იგივე ამოცანა გადავჭრათ იტერაციული ალგორითმით, რომელიც კიდევ უფრო მარტივია. ვქმნით n-ელემენტიან მასივს, რომლის პირველ და მეორე უჯრაში პირდაპირ ჩავწერთ 0-ს და 1-ს, ხოლო ყოველ შემდეგ უჯრაში წინა ორის ჯამს. ეს პროცესი გაგრძელდება მანამ, სანამ მოთხოვნილ მე-n წევრამდე არ მივალთ.

ალგორითმის ფსევდოკოდი:

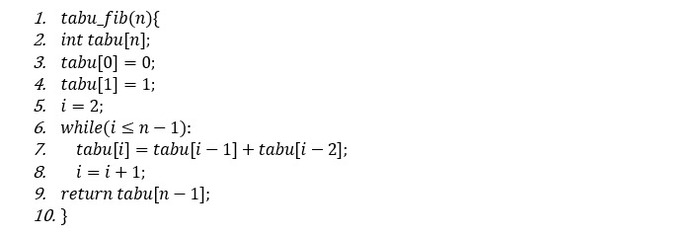
როგორც უკვე აღვნიშნეთ, დინამიკურ პროგრამირებაში გამოყოფენ კიდევ ორ ქვემიმართულებას: ტაბულაცია (Tabulation ან Bottom Up) და მემოიზაცია (Memoization ან Top Down). განვიხილოთ ორი წინადადება:

1. ჯერ უნდა ვისწავლო ბაკალავრიატზე, შემდეგ მაგისტრატურაზე, ბოლოს კი მოვიპოვებ დოქტორის ხარისხს.
2. იმისთვის, რომ მოვიპოვო დოქტორის ხარისხი, საჭიროა, დავასრულო მაგისტრატურა, ხოლო მაგისტრატურაზე ჩასაბარებლად ჯერ უნდა დავასრულო ბაკალავრიატი.

ორივე წინადადების შინაარსი ერთი და იგივეა, თუმცა განსხვავებულია მათი გადმოცემის ფორმა. პირველი შეგვიძლია გავაიგივოთ ტაბულაციასთან, იგივე აღმავალ, ხოლო მეორე მემოიზაციასთან, იგივე დაღმავალ დინამიკურ პროგრამირებასთან. როგორც წესი, მემოიზაციის გამოყენებისას ალგორითმი რეკურსიულია, ხოლო ტაბულაციისას — იტერაციული. მემოიზაცია ამოხსნას ბოლოდან იწყებს, ჩადის საბაზო ქვეამოცანამდე და შემდეგ ისევ უკან ბრუნდება პასუხის "მოსატანად". ტაბულაციის დროს კი ვიწყებთ ქვემოდან, ანუ ცხრილის (ფორმალურ ენაზე — მატრიცის) პირდაპირ, საწყისი უჯრიდანვე შევსებას და მივიწევთ ზემოთ (ამას მიუთითებს მის მეორე სახელში "აღმავალიც"). აქედან გამომდინარე, მარტივად შეგვიძლია დავასკვნათ, რომ ჩვენ მიერ ზემოთ განხილული ბოლო ორი ალგორითმიდან ორივე დინამიკურ პროგრამირებას იყენებს, თუმცა memo_fib მემოიზაციას მიმართავს, ხოლო tabu_fib — ტაბულაციას.

პასკალის სამკუთხედის წევრების პოვნა

ახლა კი განვიხილოთ პასკალის სამკუთხედი, რომელსაც მნიშვნელოვანი გამოყენება აქვს პრაქტიკაში. პასკალის სამკუთხედი სამკუთხა ცხრილია, რომლის ყოველი ელემენტი, მის ზემოთ მდგარი ორი ელემენტის ჯამის ტოლია.

მაგალითად, მე-5 სტრიქონის მე-2 ელემენტი 4-ის ტოლია, რადგან მის ზემოთ მდგომი 1-ის და 3-ის ჯამი 4-ია.

პასკალის სამკუთხედის გამოყენება შესაძლებელია ორი რიცხვის ჯამის n ხარისხში აყვანის შედეგად მიღებული მრავალწევრის კოეფიციენტების დასადგენად. დავაკვირდეთ რამდენიმე, ჩვენთვის ნაცნობ ფორმულას და შევამჩნიოთ, რომ ყოველი მრავალწევრის კოეფიციენტების მიმდევრობა, პასკალის სამკუთხედის იმ რიგს ემთხვევა რომელ ხარისხშიც აგვყავს a+b გამოსახულება. (გაითვალისწინეთ, რომ პასკალის სამკუთხედში რიგების ათვლას ნულიდან ვიწყებთ, შესაბამისად, (a+b)⁰ = 1 და პასკალის სამკუთხედშიც ნულოვან რიგში გვაქვს ერთიანი).

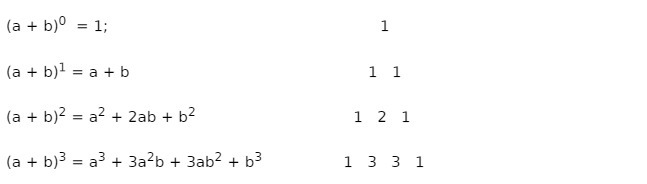
პასკალის სამკუთხედი მნიშვნელოვანია კომბინატორიკაში. კერძოდ, თუ P_{n, k} -ით აღვნიშნავთ პასკალის სამკუთხედში n-ურ სტრიქონზე k-ურ ელემენტს (მაგ.P_{4, 3} იქნება მეოთხე სტრიქონზე მესამე ელემენტი, რომლიც არის 1, რადგან როგორც სტრიქონების ათვლას ვიწყებთ ნულიდან, ასევეა სვეტებისთვისაც. მაგალითად, სამკუთხედში ყველაზე მაღლა გვაქვს ნულოვანი სტრიქონის ნულოვანი ელემენტი - 1) მაშინ მივიღებთ, რომ P_{n, k} ბინომიალურ კოეფიციენტს, ჯუფდებას აღნიშნავს. ანუ არის n ელემენტიანი სიმრავლიდან k ელემენტიანი სიმრავლეების ამორჩევის შესაძლებლობათა რაოდენობა.

მაგალითად, თუ n=3 და k=2, გამოდის, რომ გვაქვს სამ-ელემენტიანი სიმრავლე და უნდა ვიპოვოთ მისთვის რამდენი 2-ელემენტიანი ქვესიმრავლე არსებობს. ამ შემთხვევაში ასეთი სიმრავლეები იქნება: , , . ანუ გვაქვს ასეთი სამი ვარიანტი. შევნიშნოთ, რომ პასკალის სამკუთხედშიც P_{3, 2} = 3 (აუცილებლად გაითვალისწინეთ, რომ როგორც სტრიქონების, ისე სვეტების ათვლას ნულიდან ვიწყებთ).

რეალურად, კომბინატორიკაში არსებობს ფორმულა P_{n, k}= n!/(k!(n-k)!), რაც მისი გამოთვლის შესაძლებლობას პასკალის სამკუთხედის წევრების პოვნის გარეშეც გვაძლევს. მაგრამ ამ ფორმულის უდიდესი უარყოფითი მხარე ის გახლავთ, რომ შუალედურმა გამოთვლებმა შესაძლოა გამოიწვიოს არითმეტიკული გადავსება (overflow) მაშინაც კი როცა საბოლოო პასუხი (კოეფიციენტი) თავისუფლად მოთავსდება int-ში. ანუ n!-ის k!(n-k)!-ზე გაყოფისას მიღებული რიცხვი პრობლემას არ შეგვიქმნის, თუმცა გაყოფამდე, ცალკე გამოთვლილი მრიცხველი და მნიშვნელი შესაძლოა იმდენად დიდი იყოს, რომ მათი შენახვა ვერ შევძლოთ და მეხსიერების გადავსება გამოიწვიოს. სწორედ ამიტომ ხდება მნიშვნელოვანი, ბინომიალური კოეფიციენტების პასკალის სამკუთხედზე დაყრდნობით პოვნა და შესაბამისად პასკალის სამკუთხედის P_{n, k} წევრის პოვნა. ამიტომ, ვეცადოთ მისი ალგორითმის დინამიკური პროგრამირების გამოყენებით დაწერას. პირველ რიგში, უმჯობესია რიცხვებს სამკუთხედის ფორმის მაგივრად, მატრიცის მსგავსი, მართკუთხედი ფორმა მივცეთ:

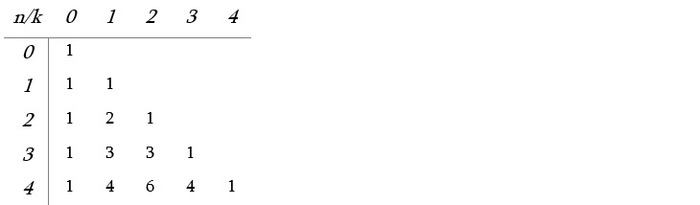
მარტივად დავინახავთ რეკურსიულ კავშირსაც, რომელიც შემდეგი ფორმულით ჩაიწერება:

P_{n, k} = P_{n-1, k-1} + P_{n-1, k}

რატომაა სამართლიანი მოცემული ფორმულა? n ელემენტიანი სიმრავლიდან ამორჩეული ყოველი k ელემენტიანი ქვესიმრავლისთვის გვაქვს ორი შემთხვევა: მასში შედის ან არ შედის n ელემენტიანი სიმრავლის მე-n ელემენტი. განვხილოთ ორივე შემთხვევა:

1) თუ მე-n ელემენტი შედის ქვესიმრავლეში (რომელსაც განვიხილავთ), მაშინ რამდენნაირად შეიძლება შეირჩეს მისი დანარჩენი წევრები? n ელემენტიანი სიმრავლიდან დაგვრჩა n-1 ელემენტიანი სიმრავლე (რადგან მე-n ელემენტი უკვე ქვესიმრავლეში გვყავს შეყვანილი), და აქედან ამოსარჩევია k-1 ელემენტიანი სიმრავლეები (1 ადგილი მე-n ელემენტს უკვე დაკავებული აქვს). ანუ გამოდის, რომ n ელემენტიანი სიმრავლიდან, k ელემენტიანი ისეთი ქვესიმრავლეების ამორჩევის შესაძლებლობა, რომლებშიც n ელემენტიანი სიმრავლის მე-n ელემენტი შედის, P_{n-1, k-1} -ს ტოლია.

2) ხოლო, თუ მე-n ელემენტი არ შედის ქვესიმრავლეში, n ელემენტიანი სიმრავლიდან დაგვრჩა ისევ n-1 ელემენტიანი სიმრავლე (რადგან დანამდვილებით ვიცით, რომ მე-n ელემენტი ქვესიმრავლეში არ შედის), თუმცა ამჯერად ამოსარჩევი გვაქვს k ელემენტიანი ქვესიმრავლე (წინა შემთხვევისგან განსხვავებით აქ ერთი ადგილი მე-n წევრს აღარ უჭირავს, რადგან ქვესიმრავლეში არ შედის). ანუ გამოდის, რომ n ელემენტიანი სიმრავლიდან, k ელემენტიანი ისეთი ქვესიმრავლეების ამორჩევის შესაძლებლობა, რომლებშიც n ელემენტიანი სიმრავლის მე-n ელემენტი არ შედის, P_{n-1, k} -ს ტოლია.

ჩვენ განვიხილეთ ყველა შესაძლო P_{n, k} ვარიანტი, რომელიც ტოლია ისეთი ქვესიმრავლეების რაოდენობის ჯამისა, სადაც მე-n ელემენტი შედის, ან არ შედის. ზემოთ კი ორივეს რაოდენობა დავთვალეთ და ფორმულის სამართლიანობაც დამტკიცდა.

ალგორითმის დაწერამდე აუცილებელია დავადგინოთ საბაზისო შემთხვევები. რომელი ბინომიალური კოეფიციენტები შეგვიძლია განვსაზღვროთ წინასწარ, მათი გამოთვლის გარეშე? ბუნებრივია, ნებისმიერ ელემენტიანი სიმრავლიდან 0-ელემენტიანი ქვესიმრავლეების (გვექნება მხოლოდ ცარიელი სიმრავლე) რაოდენობა 1-ის ტოლია (P_{n, 0}=1). ამავე დროს, n-ელემენტიანი სიმრავლიდან n-ელემენტიანი ქვესიმრავლეების რაოდენობაც 1-ის ტოლია (P_n,n=1). ამიტომ, ალგორითმის გაშვებამდე, ყოველი i-ური სტრიქონის ნულოვან და i-ურ ინდექსებზე მდგომი უჯრები 1-ს უნდა გავუტოლოთ. დანარჩენი წევრების გამოთვლას კი რეკურსიული ფორმულით უპრობლემოდ შევძლებთ.

ალგორითმის ფსევდოკოდი:

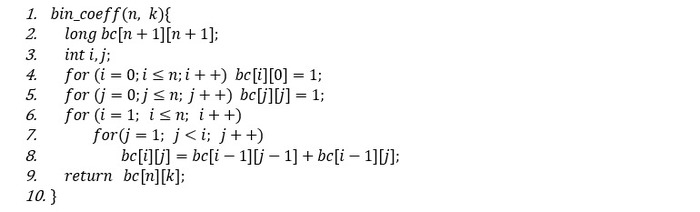
მოცემული აგორითმის უკეთ გასააზრებლად შეგიძლიათ განიხილოთ ამოცანის კონკრეტული მაგალითი (მაგ. n=5, k=4) და ჩაატაროთ ტრასირება, ანუ განახორციელოთ მისთვის ალგორითმის ყოველი ბიჯი და დააკვირდეთ მისი ამოხსნის პროცესს.

Challenge: სცადეთ იგივე ამოცანისთვის რეკურსიული ალგორითმის დაწერა. საბაზო შემთხვევისთვის გაითვალისწინეთ შემოწმება: if ( n==0 ან n==k) return 1;

ოპტიმიზაციის ამოცანები

დასაწყისში აღვნიშნეთ, რომ დინამიკური პროგრამირება ძალიან მნიშვნელოვანი მეთოდია ოპტიმიზაციის ამოცანების ამოსახსნელად, როდესაც ამოცანას შესაძლოა რამდენიმე ამონახსნი ჰქონდეს, თუმცა გვთხოვენ მათ შორის რაღაც თვალსაზრისით ოპტიმალური ვარიანტის (მინიმალურის ან მაქსიმალურის) ამორჩევას. ზემოთ განხილულ ამოცანებში კი მხოლოდ ერთადერთი შესაძლო ამონახსნი არსებობდა და არც რაიმეს ოპტიმიზაციას ვახდენდით.

განვიხილოთ პირველი ოპტიმიზაციის ამოცანა:

მოცემულია n - ცალი მონეტის მწკრივი. თითოეულის ღირებულება რაიმე დადებითი მთელი რიცხვის ტოლია: c₁, c₂ ... c_n. ჩვენი მიზანია ავკრიფოთ ისეთი მონეტები რომელთა ჯამური ღირებულება მაქსიმალური იქნება, თუმცა იმ შეზღუდვით, რომ არ შეგვიძლია ორი ერთმანეთის მიმდევრობით განთავსებული (მოსაზღვრე) მონეტების აღება.

ვთქვათ, F_n იყოს მაქსიმალური თანხა, რაც შეიძლება მოპოვებული იქნას n-ცალი მონეტიანი მწკრივიდან. რეკურსიული კავშირის საპოვნელად, მონეტების არჩევის ყველა დასაშვები შესაძლებლობა დავყოთ ორ ჯგუფად: ისინი, რომლებიც მოიცავენ ბოლო (მე-n) მონეტას და ისინი, რომლებიც არ მოიცავენ. მაქსიმალური თანხა რისი მიღებაც პირველი ჯგუფიდან შეგვიძლია არის c_n+F_n-2 - მე-n მონეტის ღირებულებას დამატებული მაქსიმალური მოგება რისი მიღებაც პირველი n-2 მონეტისგან შეგვიძლია ((n-1)-ე მონეტას უკვე ვეღარ ავიღებთ, რადგან ის მე-n მონეტის მოსაზღვრეა და პირველ ჯგუფში, როგორც შევთანხმდით, მე-n მონეტა შედის). ხოლო მეორე ჯგუფიდან მიღებული მაქსიმალური მოგება F_n-1 იქნება, რადგან ამ არჩევანში არ შედის მე-n მონეტა, შესაბამისად მოგება დარჩება იგივე, რაც იყო პირველი n-1 წევრისთვის. მოცემული მსჯელობით ვიღებთ რეკურსიულ ფორმულას:

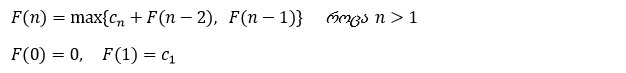
მოცემული ფორმულით შეგვიძლია გამოვთვალოთ F(n) და შევავსოთ მასივი, როგორც ეს tabu_fib(n) ალგორითმისთვის გავაკეთეთ:

ალგორითმის ფსევდოკოდი:

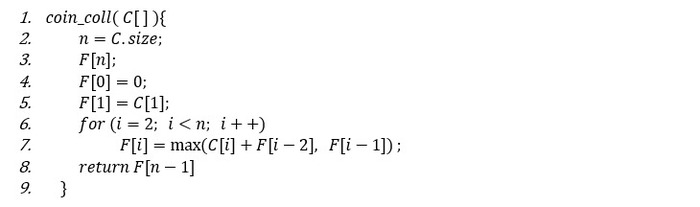
განვახორციელოთ ალგორითმის ტრასირება კონკრეტული მონაცემებისთვის. ჩავთვალოთ, რომ შემავალი C მასივის ნულოვან ინდექსზე მნიშვნელობა არ გვაქვს (ან შეგვიძლია 0-ის ტოლად მივიჩნიოთ), ამით მონეტის ღირებულება დაემთხვევა მის რიგობრივ ნომერს მწკრივში (რიგობრივი ნომერი იქნება ინდექსი) და უფრო მარტივად აღსაქმელი გახდება.

ჩვენი ამოცანისთვის მივიღეთ, რომ მაქსიმალური მოგება იქნება 12, თუმცა საინტერესოა ამ მოგების მისაღებად რომელი მონეტები უნდა ავიღოთ. ოპტიმიზაციის ამოცანებში ეს საკითხი ხშირად დგას და ამოცანის ამოხსნის მეორე ნაწილია. დინამიკური პროგრამირებით ამოხსნისას ჩვენ გვეძლევა საშუალება, აღვადგინოთ გზა (ამონახსნი), რომლითაც ოპტიმალურ მნიშვნელობამდე მივედით, ანუ ჩვენს შემთხვევაში შეგვიძლია ვიპოვოთ ის მონეტები, რომელთა ჯამური ღირებულება 12-ის ტოლი იქნება. მათ საპოვნელად მოქმედებას ვიწყებთ ბოლოდან, ანუ F_n უჯრიდან: თუ C_n + F_n-2 > F_n-1 ეს იმის მანიშნებელია, რომ ამონახსნში (ასაკრები მონეტების სიმრავლეში) მე-n მონეტაც უნდა შეგვეყვანა. თუ C_n+ F_n-2 < F_n-1 მე-n მონეტის შეყვანა წამგებიანი იქნებოდა და ამიტომ მას დავტოვებდით. ხოლო თუ C_n + F_n-2 = F_n-1, ეს ის შემთხვევაა როცა აზრი არ აქვს შევიყვანთ თუ არა მე-n მონეტას, რადგან მოგება ორივე შემთხვევაში, ერთნაირი გვექნება. შესაბამისად, ოპტიმალური ამონახსნის სიმრავლის პოვნის ალგორითმი მიიღებს შემდეგ სახეს:

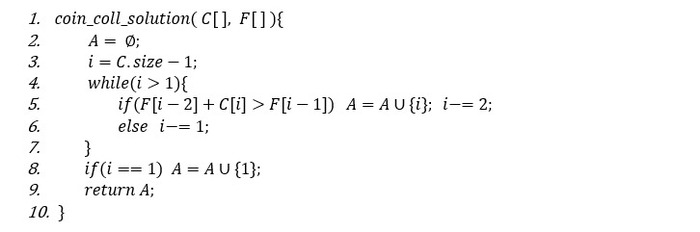
თუ ზემოთ, ჩვენ მიერ განხილული ამოცანისთვით ამ ალგორითმს გავუშვებთ, ის დაგვიბრუნებს სიმრავლეს, რაც ნიშნავს, რომ მაქსიმალური მოგების მისაღებად და ჩვენი შეზღუდვის გათვალისწინებით, საჭიროა მე-2 და მე-4 მონეტების აღება.

Challenge: იგივე ამოცანისთვის სცადეთ coin_coll და coin_coll_solution ფუნქციების რეკურსიული სახით იმპლემენტაცია.

---

როგორც უკვე ვახსენე, დინამიკური პროგრამირებას ოპტიმიზაციის ამოცანების ამოხსნაში განსაკუთრებული როლი უჭირავს და გვეხმარება გავაუმჯობესოთ ალგორითმის მუშაობის დრო. ამას ის მართლაც კარგად ასრულებს, თუმცა სამაგიეროდ გვართმევს დიდი რაოდენობის მეხსიერებას. მაგალითად, ალგორითმში, სადაც მოცემული გვქონდა C მასივი, ქვეამოცანების ამონახსნების შესანახად საჭირო გახდა ამავე ზომის F მასივის შემოტანაც. ამიტომ, დიდი მონაცემების შეტანისას დინამიკური პროგრამირების ნაკლი, დიდი მეხსიერების დანახარჯია.

თუ სტატიაში განხილული თემა და ზოგადად, მეცნიერებისა და ტექნოლოგიების სფერო შენთვის საინტერესოა, შემოგვიერთდი ჯგუფში – შემდეგი ჯგუფი.