სიცოცხლის თამაში დამწყებთათვის: რატომაა მათემატიკა ასეთი თვალწარმტაცი

სიცოცხლის თამაში ორგანზომილებიანი სამყაროა, სადაც დროთა განმავლობაში კანონზომიერებები წარმოიქმნება. ის ძალიან კარგი ილუსტრაციაა იმისა, რომ უმარტივეს სამყაროშიც კი, სადაც ძალიან ცოტა წესია, სიმარტივიდან ძალიან დახვეწილი, რთული და ამასთანავე ლამაზი კანონზომიერებები ჩნდება. ამ თამაშის განსაკუთრებულობა იმაშიცაა, რომ განსაზღვრული მიზანი არ გააჩნია.
სიცოცხლის თამაშის სამყარო ძალიან მარტივია: წარმოიდგინეთ კვადრატული უჯრების მქონე ზედაპირი, სადაც გაფერადებული უჯრა ცოცხალ უჯრედს ასახავს, ხოლო თეთრი — მკვდარს. ამ ორგანზომილებიან სამყაროში სიცოცხლეს რამდენიმე წესი აქვს.
წესები ცოცხალთათვის:
- ცოცხალი უჯრედი, რომელსაც ორზე ნაკლები ცოცხალი მეზობელი ჰყავს მოკვდება.
- ცოცხალი უჯრედი, რომელსაც ორი ან სამი ცოცხალი მეზობელი ჰყავს, გადარჩება.
- ცოცხალი უჯრედი, რომელსაც ოთხი ან მეტი ცოცხალი მეზობელი ჰყავს, მოკვდება.
წესები მკვდრებისთვის:
- მკვდარი უჯრედი, რომელსაც სამი ცოცხალი მეზობელი გაუჩნდება, ცოცხლდება.
- სხვა ყველა შემთხვევაში, უჯრედი მკვდარი რჩება.
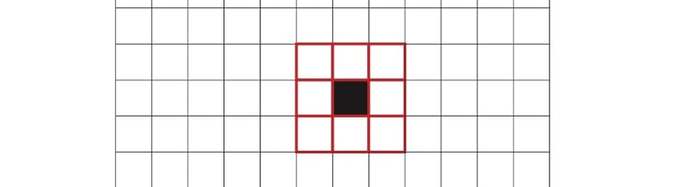
ყველა უჯრედს ზუსტად 8 მეზობელი ჰყავს
თამაში უჯრის ან უჯრების მონიშვნით იწყება, რის შედეგადაც მონიშნული უჯრები შავდება და ჩნდება 0 თაობის უჯრედი ან უჯრედები. სიმულაციის გააქტიურებისას ბადეზე ზემოხსენებული წესები მოქმედებს და უჯრედები კონფიგურაციას იცვლიან, ცვლილება შემდეგ (პირველ) თაობას ბადებს, ამის მერე პირველ თაობაზე იგივე წესები მოქმედებს და შედეგად უკვე მე-3 თაობა იბადება და ა.შ მარადიულად
სულ ესაა.
თამაში ბრიტანელმა მათემატიკოსმა ჯონ კონვეიმ 1960-იან წლებში მოიგონა. მან წესები ისე შეარჩია, რომ სიმულაციაში რთულად წინასწარმეტყველებადი კანონზომიერები წარმოქმნილიყო. მოდი რამდენიმე კანონზომიერება მოკლედ მიმოვიხილოთ.
უძრავი სიცოცხლეები

ბლოკი
ეს უძრავი სიცოცხლის ყველაზე მარტივი ფორმა — ბლოკია. ფოტოზე ხედავთ, რომ გაფერადებული მხოლოდ ოთხი მოსაზღვრე (ანუ მეზობელი) უჯრაა. აქ თითოეულ უჯრას 3 მეზობელი ჰყავს, ანუ არცერთი უჯრედი არ კვდება და უჯრედთა სისტემა გაჩერებულია.

მეორე ფოტოზე თქვენ უძრავ სკას ხედავთ. ბლოკის მსგავსად აქაც სიცოცხლის მეორე წესი მოქმედებს. ანუ, ყველა უჯრედს მინიმუმ ორი მეზობელი ჰყავს, შესაბამისად, მოძრაობა აქაც არ წარმოიქმნება.
ოსცილატორები

ციმციმა
ციმციმა ყველაზე მარტივი ცოცხალი სისტემაა. თუ მონაკვეთზე მიყოლებით სამ უჯრას მონიშნავთ და სიმულაციას გაუშვებთ, ასეთ შედეგს მიიღებთ. იმიტომ, რომ ამ შემთხვევაში განაპირა უჯრედებს მხოლოდ ერთ მეზობელი ყავთ, შესაბამისად ისინი მოკვდებიან და მხოლოდ ცენტრალური უჯრედი დარჩება.
გაიხსენეთ, რომ თუ მკვდარ უჯრედს (ანუ თეთრ უჯრას) სამი ცოცხალი მეზობელი ჰყავს, ის [მკვდარი უჯრედი] გაცოცხლდება. სამუჯრიანი მონაკვეთის გავლების შემთხვევაში, ცენტრალურ უჯრედს სამხრეთით და ჩრდილოეთით მდებარე მკვდარ უჯრედებს, გამოდის რომ სამი მოსაზღვრე მეზობელი ყავთ, რაც მათ [მკვდარ უჯრედებს] გააცოცხლებს.

პულასრი
სამი უჯრედის შემთხვევაში ყველაფერი მარტივად ჩანს, თუმცა რთული ოსცილატორების შექმნაც შეგვიძლია. მაგალითად, ეს პულსარია. თუ რატომ მოძრაობს უჯრედების სისტემა ასე, ახსნას არ დავიწყებ, ზედმეტად ბევრი ცვლადია. თუმცა, შეგიძლიათ უბრალოდ სანახაობით დატკბეთ.
ხომალდები

გლაიდერი
ამ ფოტოზე თქვენ ყველაზე მარტივ ხომალდს, გლაიდერს ხედავთ. სიცოცხლის თამაშში უჯრების სწორად შერჩევით მოძრაობის შექმნაც შეგიძლიათ. ანუ, უჯრები ისე შეგიძლიათ გააფერადოთ, რომ გადაადგილების ილუზია შეიქმნას. ეს რაღაცით პროგრესული მატრიცების ტესტს წააგავს.

მძიმე წონის ხომალდი
მეტი უჯრის გაფერადებით, ანუ მეტი უჯრედის არსებობის შემთხვევაში, კანონზომიერება ნელ-ნელა ბევრად რთულად წინასწარმეტყველებადი ხდება. ჩემი აზრით, თამაშის ხიბლი სწორედ აქ იმალება.
რატომაა არის ეს თამაში საინტერესო
- სიცოცხლის თამაშში მოქმედი კანონების გამო ცოცხალ უჯრედთა ზოგ სისტემას გარკვეული შეზღუდვები აქვს. მაგალითად, 5-უჯრედიანი სისტემების (მე პირადად სისტემებს ცხოველებს ვეძახი ხოლმე) მეხუთე თაობა კვდება ან უძრაობას აღწევს. გამონაკლისი ეგრეთ წოდებული R-pentomino-ს სისტემაა, რომელიც მოძრაობას 1 000 თაობის მანძილზე აგრძელებს.
თამაშით დაინტერესებული მეცნიერები სხვადასხვა კანონზომიერების ძიებას შეუდგნენ. მაგალითად, როცა კონვეიმ სიცოცხლის თამაშის წესები შექმნა, ის დარწმუნებული არ იყო, რომ იარსებებდა კანონზომიერება, სადაც ცოცხალი უჯრედების რაოდენობა დროთა განმავლობაში გაიზრდებოდა.
MIT-ში მომუშავე მათემატიკოსმა, ბილ გოსპერმა, ხანგრძლივი მუშაობის შემდეგ ამ კითხვას დადებითად უპასუხა. მან ეგრედწოდებული "გლაიდერის თოფი" შექმნა, ანუ სისტემა, რომელიც 30 თაობაში ერთხელ ახალ გლაიდერს წარმოქმნის. ეს პროცესი კი უსასრულოდ გრძელდება.
გოსპერმა ასევე შექმნა სისტემა, სადაც ცოცხალი უჯრედების რაოდენობა ყოველ მომდევნო თაობაში უფრო სწრაფად იზრდება.

ქაოტურად დაწყებული მოძრაობა უფრო და უფრო მოწესრიგებული ხდება და ბოლოს ფიბონაჩის კანონზომიერების მაგვარ ვიზუალს წარმოქმნის.
მეცნიერება კანონზომიერების ძიებაა
პრაქტიკულად ნებისმიერი საბუნებისმეტყველო დარგის მეცნიერებაში მიმდინარე კვლევებს თუ დააკვირდებით, აღმოაჩენთ, რომ სიმეტრიას მეცნიერებაში მნიშვნელოვანი ადგილი უჭირავს. ქაოტურ მოვლენებს მიღმა, შესაძლოა ელეგანტური კანონზომიერება იმალებოდეს.
კონვეის სიცოცხლის თამაშით კომპიუტერის მუშაობის მექანიზმის აღწერა სურდა. ამისთვის სიცოცხლის თამაში კომპიუტერის საბაზისო "ლოგიკური ბრძანებების" (არა, და, კი) ერთგვარი ანალოგია.
სიცოცხლის თამაშში მონაწილეობის მიღება თქვენც შეგიძლით, ის უფასოა და მის ჩაწერას ამ საიტიდან შეძლებთ.












კომენტარები