რა არის დრო? ყველას და ყველაფერს ჩვენ ირგვლივ გარკვეული მიმართულება აქვს — საგნები და ადამიანები ჩვენ ირგვლივ გადაადგილდებიან წარსულიდან მომავალში და არა პირიქით. ეს ერთი შეხედვით ბუნებრივი მოცემულობა თეორიული ფიზიკოსებისთვის დიდი თავსატეხია, რადგან ფიზიკის კანონების უმრავლესობა დროის თვალსაზრისით სიმეტრიულია, ისინი არ განარჩევენ ერთმანეთისგან წარსულსა და მომავალს. ითვლება, რომ დროის ისარი მიმართულებას თერმოდინამიკის კანონების, კერძოდ მეორე კანონის (ენტროპია ყოველთვის იზრდება) მეშვეობით იძენს. ჩვენ გვახსოვს წარსული და არა მომავალი, ვბერდებით და არ ვახალგაზრდავდებით, იმავე მიზეზის გამო, რა მიზეზითაც ცხელი ყავა სპონტანურად გრილდება და არა პირიქით.

თუმცა, რამდენად უნივერსალურია მეორე კანონი? თერმოდინამიკა როგორც დარგი წარმოიშვა ინდუსტრიული რევოლუციის გარიჟრაჟზე, როგორც ძრავის ეფექტიანობის გაზრდის მცდელობა და მისი კანონები აღწერს სისტემის ქცევას შემოფარგლულ სივრცეებში. რამდენად სამართლიანია მისი განზოგადება კოსმოლოგიამდე იმის გათვალისწინებით, რომ თერმოდინამიკის შემქმნელებს წარმოდგენა არ ჰქონდათ იმ ფაქტის შესახებ, რომ სამყარო ფართოვდება? იზრდება თუ არა სამყაროს ენტროპია მთლიანობაში?

თეორიული ფიზიკოსის, ჯულიან ბარბორის ნაშრომი "იანუსის წერტილი" სწორედ ამ საკითხს შეეხება. მასში გადმოცემული იდეები რადიკალურად ცვლის ჩვენ წარმოდგენებს კოსმოლოგიაზე — მისი თეორიის თანახმად დიდი აფეთქება უნდა აღვიქვათ არა როგორც სამყაროს დაბადება განსაკუთრებული დაბალ-ენტროპიული მდგომარეობიდან, არამედ წერტილი დროის ხაზზე, რომლის ორივე მხარესაც ორი სამყარო ვითარდება და იზრდება კომპლექსურობაში უკიდურესად ერთგვაროვანი მდგომარეობიდან.

ჯულიან ბარბორის იდეები კოსმოლოგიის რადიკალურ გადასინჯვას მოითხოვს, მაგრამ მისი ორიგინალურობა მხოლოდ ამაში არ მდგომარეობს, არამედ მეცნიერების მიმართ მის დამოკიდებულებაშიც ვლინდება: აინშტაინის ფარდობითობის ზოგადი თეორიის შესახებ სადოქტოროს დაცვის შემდეგ, მან უარი თქვა აკადემიურ თანამდებობაზე და თავის იდეებზე სამუშაოდ ჩრდილოეთ ნოქსფორდშირის სოფელში გადავიდა საცხოვრებლად. ის არ ეთანხმება თანამედროვე აკადემიურ სისტემის კონვეიერულ ხასიათს, რომელიც სთხოვს მკვლევარს, გამოაქვეყნოს ტექნიკური სტატიების გარკვეული რაოდენობა წელიწადში (გამოაქვეყნე ან გაქრი მიდგომა), რადგან თვლის, რომ ფუნდამენტური იდეებზე ფიქრს შეიძლება წლები დასჭირდეს.

ჯულიან ბარბორის წიგნები და ესეები თავმოყრილია მის ვებსაიტზე, ქვემოთ კი მასთან ინტერვიუს გთავაზობთ.

ჯულიან, დავიწყოთ დროის ისრის კონცეფციის მოკლე მიმოხილვით. რა არის დროის ისარი და რა სახის ისრები არსებობს?

ყველაზე აშკარაა ისარი, რომელსაც ყოველი ჩვენგანი აღიქვამს. ყველას გვაქვს შეგრძნება, რომ დრო გადის, გვაქვს წარსულის მოგონებები და არა მომავლის. ფიზიკურ დონეზე, ყველა ვბერდებით ერთი მიმართულებით და ვერავის იპოვით, ვინც ახალგაზრდავდება. ეს საკმაოდ გავრცელებული რამაა მთელ სამყაროში. ასტრონომები დღეს იკვლევენ ვარსკვლავების ევოლუციას და ვარსკვლავებიც იმავე მიმართულებით ბერდებიან, საითაც ჩვენ. ეს საკითხი 1850-იანებში წამოიჭრა თერმოდინამიკის კანონების აღმოჩენასთან ერთად, რადგან ნიუტონის კანონები დროის შებრუნების მიმართ სიმეტრიულია (Time-Reversal Symmetry), ისინი ერთნაირად კარგად მუშაობენ ორივე მიმართულებით.

წარმოიდგინე, რომ გაქვს ნაწილაკები, რომლებიც ვითარდებიან გარკვეული საწყისი მდგომარეობებიდან ნიუტონის კანონების შესაბამისად და რაღაც ეტაპზე, წარმოვიდგინოთ, რომ მყისიერად შემოვაბრუნეთ ნაწილაკების სიჩქარეები ისე, რომ პოზიციები უცვლელად დავტოვეთ. მაშინ ეს გარდაიქმნება საწყის მდგომარეობებად ახალი ამონახსნისთვის. ნაწილაკები თავიანთ ევოლუციას უკუღმა გავლიან და იმავე ტრაექტორიას გაჰყვებიან. ეს ნიუტონის კანონების არსებითი ასპექტია და ის მიემართება ბუნების თითქმის ყველა სხვა კანონს, რამდენიმე გამონაკლისის გარდა.

კიდევ ერთი ისარია ელექტრომაგნიტური ტალღების ქცევა. წარმოიდგინე სატელევიზიო ანტენა, რომელიც გზავნის რადიო სიგნალებს ან სატელევიზიო სიგნალებს. ისინი გამოეყოფიან ანტენას სფერული ტალღების სახით, მაგრამ ისინი არასდროს ბრუნდებიან უკან ანტენაში. იგივე ფენომენია, როცა გუბურაში ქვას ჩააგდებ და წრიული ტალღები დაცემის წერტილიდან გარეთ ვრცელდება, ვიდრე გუბურის კიდეს მიაღწევს.

კიდევ ერთი მაგალითი, რაც უკვე ვახსენე — ჩვენ გვახსოვს ჩვენი წარსული, რაც თანხვედრაშია არა მხოლოდ შენივე ცნობიერთან, არამედ სხვა ადამიანების გამოცდილებასთანაც. ამას ფსიქოლოგიური ისარი ეწოდება.

კვანტურ მექანიკაში არსებობს თავსატეხი, ტალღური ფუნქციის კოლაფსი. დეტალებში არ შევალ, რადგან ტექნიკური საკითხია. დარწმუნებული ვარ ადამიანები, რომლებსაც კვანტური მექანიკის დაინტერესებულან, სმენიათ შროდინგერის კატის შესახებ. კვანტურ მექანიკაში შეიძლება გვქონდეს სიტუაცია, სადაც კატა არის ყუთში, რომელშიც საწამლავის შემცველი ჭურჭელი გატყდა ან არ გატყდა. ანუ ორი შესაძლებლობაა, რომელიც ერთდროულად არსებობს, ერთში კატა მკვდარია, ხოლო მეორეში კატა ცოცხალია. კვანტური მექანიკის თანახმად, ვიდრე არ ჩაიხხედები ყუთში, ორივე შესაძლებლობა არსებობს და კვანტური მექანიკის გაგება შეუძლებელია ამ დაშვების აღიარების გარეშე. შემდეგ, როცა თავსახურს ახდი და ჩაიხედები, ერთ-ერთ შესაძლებლობას აწყდები და ამას ტალღური ფუნქციის კოლაფსი ეწოდება. ამის თაობაზე უსასრულო დისკუსიები მიმდინარეობს და უთვალავი სტატია დაწერილა.

ვახსენებ დროის კიდევ ერთ ისარს, რომელიც ყველაზე მნიშვნელოვანია ჩემი ნაშრომის კონტექსტში. ესაა დროის თერმოდინამიკური ისარი — ენტროპია. ენტროპია განიმარტება, როგორც უწესრიგობის ზომა. თუ გაქვს ყუთი, რომლის ერთ-ერთ კუთხეში ყინულის ბლოკი დევს. ყინული თანდათან გალღვება და მივიღებთ წყალს, რომელიც ერთგვაროვნად განაწილდება ყუთში. ერთგაროვნება კიდევ უფრო გაიზრდება, თუ წყალი აორთქლდება და ყუთის ყველა ნაწილში თანაბრად განაწილდება. ამას შეუქცევადი პროცესი ეწოდება. თეორიულად, თუ წარმოვიდგენთ, რომ ყველა ნაწილაკის სიჩქარეების საპირისპირო მიმართულებით შემობრუნება შეგვიძლია, ისინი სპონტანურად თხევადი მდგომარეობიდან ყინულის ნატეხად გარდაიქმნებოდნენ, მაგრამ ეს ბუნებაში არასდროს ხდება. უწესრიგობის ზომას, რომელიც იზრდება მოწესრიგებული ყინულის კრისტალური სტრუქტურიდან თხევად მდგომარეობამდე, ენტროპიის ზრდა ეწოდება. მეცნიერების თანახმად, ეს არის ყველაზე ფუნდამენტური დროის ისარი.

დღეს არსებული ფართო კონსესუსი თანახმად, ენტროპიის ზრდის გამო, სამყარო სითბური სიკვდილის მდგომარეობისკენ მიისწრაფის. ბევრი მეცნიერის აზრით, ენტროპია მიემართება სამყაროს კოსმოლოგიურ დონეზე. თქვენ ამას არ ეთანხმებით, შეგიძლიათ აგვიხსნათ რატომ?

მეცნიერებაში არაფერია ქვაზე ამოკვეთილი. ყველა თეორია დროებითია და შემოწმებას ექვემდებარება. მე და ჩემმა კოლეგებმა ვაჩვენეთ, რომ არსებობს დროის ისრის ახსნა, რომელიც არაა კავშირში ენტროპიის ზრდასთან, ან უწესრიგობის ზრდასთან, არამედ პირიქით, დროის ისარი შეესაბამება წესრიგის ზრდას. თერმოდინამიკის კანონები აღმოაჩინეს ორთქლის ძრავის შესწავლის შედეგად. პირველი მცდელობა იყო 1824 წელს სადი კარნოს მიერ დაწერილი შესანიშნავი წიგნი, სადაც მან დაადგინა ორთქლის ძრავის მაქსიმალური თეორიული ეფექტიანობა. ამ ნაშრომმა, გამოქვეყნებიდან 26 წლის შემდეგ, უილიამ ტომპსონი, იგივე ლორდ კელვინი და გერმანელი რუდოლფ კლაუსიუსი მიიყვანა თერმოდინამიკის ორი კანონის აღმოჩენამდე. თერმოდინამიკის პირველი კანონი ამბობს, რომ ენერგია ინახება. ეს ფიზიკის სტანდარტული ნაწილია. უფრო საინტერესოა მეორე კანონი, რომელიც ენტროპიის განსაზღვრის საშუალებას გვაძლევს. მეორე კანონი ამბობს, რომ ენტროპია ვერ შემცირდება და როგორც წესი, იზრდება. ამრიგად, ყველაზე მარტივი ფორმით, რომელიც კლაუსიუსმა გამოთქვა, სითბო არ მიედინება სპონტანურად ცივი სხეულიდან ცხელისკენ. სითბო ყოველთვის ცხელიდან ცივი სხეულისკენ გადაადგილდება. თუ თბილად ხარ და გარეთ ცივ ამინდში გახვალ, შენ დაკარგავ სითბოს, რომელიც ჰაერს გადაეცემა. თუმცა, თემროდინამიკის მეორე კანონის შესახებ ყველა თეორიული დისკუსია განიხილავს ყუთში მოთავსებულ სისტემებს, როგორიცაა გალღობადი ყინულის ბლოკი, რომელზეც ვსაუბრობდი. თუ საუბარია შემოფარგლულ სისტემაზე, ყოველგვარი განსხვავება თანდათან ერთგვაროვნებაში გადაიზრდება, რასაც სითბური სიკვდილი ეწოდება.

მაგრამ, საოცარია, რომ ამ დისკუსიის 170 წლის ისტორიის განმავლობაში, არავის შეუნიშნავს, რომ შესაძლოა ყუთი საერთოდ არ არსებობდეს, როცა მთლიან სამყაროზე გვაქვს საუბარი. იქნებ სამყარო არაა ყუთში. თერმოდინამიკა ნამდვილად მყარი მეცნიერებაა, თუ შესაბამის პირობებს მივუსადაგებთ. აინშტაინმა თქვა, რომ თერმოდინამიკა ერთადერთი უნივერსალური თეორიაა, რომელშიც დარწმუნებული იყო, რომ მისი ფუნდამენტური კონცეფციების გამოყენების ფარგლებში, არასდროს გამცდარდებოდა. ამრიგად, კითხვაა, რა არის ის პირობები, რომლებსაც თერმოდინამიკა მიესადაგება? თერმოდინამიკა პირველად დამტკიცდა ორთქლის ძრავთან მიმართებაში, სადაც ორთქლი ცილინდრის ფარგლებში უნდა ყოფილიყო მოთავსებული. თუ ის გამოჟონავს ცილინდრიდან, ორთქლის ძრავი ჩერდება. როდესაც კლაუსიუსმა, ჯეიმს კლარკ მაქსველმა, ბოლცმანმა და სხვებმა განავითარეს სტატისტიკური მექანიკა (თერმოდინამიკური ქცევის ახსნა ატომების და მოლეკულების მოძრაობით), ყველა ეს თეორიული ნაშრომი იწყებოდა დაშვებით, რომ გვაქვს ისეთი სისტემა, როგორიცაა ვთქვათ ელასტიური ბურთები, რომლებიც ყუთში ქაოტურად დახტიან და ყუთის ერთი კუთხიდან ერთგვაროვნად ვრცელდებიან მთელ ყუთში. ამრიგად, ვფიქრობ ესაა პირობები, რომლებშიც თერმოდინამიკის საბაზისო კონცეფციები ვალიდურია. საოცარია, რომ თითქმის არავის, მათ შორის არც აინშტაინს, არ უფიქრია, თუ რა არის ის პირობები, რომლებსაც თერმოდინამიკური კონცეფციები შეესაბამება. ვფიქრობ, ეს პირობებია შემოფარგლული სისტემები. სამყარო ფართოვდება და ამჟამინდელი მტკიცებულებების თანახმად, ამ გაფართოების სიჩქარე იზრდება, რაც არაფრით ჰგავს ყუთში არსებულ შემოფარგლულ სისტემას.

თქვენი თეორია კოსმოლოგიაზე ჩვენი წარმოდგენების გარდაქმნას მოიაზრებს. მაგალითად, რომ დიდი აფეთქება უნდა განვიხილოთ არა როგორც სამყაროს საწყისი განსაკუთრებული დაბალ-ენტროპიული მდგომარეობა, არამედ როგორც წერტილი დროის ხაზზე, რომლის ორივე მხარესაც სამყარო ვითარდება...

მარტივი რაღაცით დავიწყოთ. მე და ჩემმა კოლეგებმა 2014 წელს გამოვაქვეყნეთ სტატია, სადაც ვიხელმძღვანელეთ არა აინშტაინის ფარდობითობის ზოგადი თეორიით, არამედ ნიუტონის გრავიტაციის უნივერსალური თეორიით. წარმოიდგინე წერტილოვანი ნაწილაკები, რომლებიც ურთიერთქმედებენ ერთმანეთთან უნივერსალური გრავიტაციის კანონის მიხედვით. ჩვენ ვისარგებლეთ ფაქტით, რომელიც 1772 წლიდანაა ცნობილი.

თუ გაქვს ნაწილაკების გარკვეული n რაოდენობა სივრცეში, ეს შეიძლება განვიხილოთ, როგორც სამყაროს მარტივი მოდელი. 1772 წელს დიდმა ფრანგმა-იტალიელმა მათემატიკოსმა, ლა გრანჟმა აჩვენა, რომ თუ ენერგია უარყოფითი არაა, ანუ ენერგია ან ნულის ტოლია ან დადებითია, მაშინ მარტივად შეგვიძლია ერთი ძალიან საინტერესო ფაქტის დამტკიცება. არსებობს სიდიდე სახელად ინერციის მომენტი, რომელიც ამ სამყაროს ზომას გვეუბნება. წარმოიდგინე, რომ გვაქვს დროის ხაზი, ნიუტონიანისეული აზრით, სადაც ერთი მიმართულება წარსულია და მეორე მიმავალი. რეზულტატი ისაა, რომ უსასრულო წარსულში სისტემის ზომა უსასრულოდ დიდი იქნებოდა და ეტაპობრივად მცირდება მინიმალურ დონემდე, შემდეგ კი ისევ იზრდება უსასრულობამდე. მინიმალური ზომის ამ წერტილს მე "იანუსის წერტილს" ვუწოდებ, რადგან ეს ჰყოფს მთლიან დროის ხაზს ორ ნახევრად. რომაული ღმერთი იანუსი ორივე მიმართულებით ერთდროულად იხედება, ამიტომაც იანუსის წერტილს ვუწოდებ.

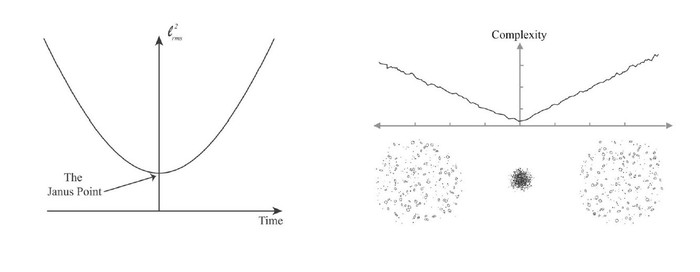
საინტერესოა, რომ ამ დრომდე, ყველა ცდილობდა აეხსნა დროის ისარი ენტროპიის ზრდით, რაც მოიაზრებს იმას, რომ სამყარო უნდა დაწყებულიყო განსაკუთრებული დაბალ-ენტროპიული მდგომარეობით, რომელიც ვერ აიხსნებოდა ბუნების არსებული კანონებით და დამატებით უნდა ყოფილიყო შემოტანილი. ცნობილი ფიზიკოსი რიჩარდ ფეინმანი ამბობდა, რომ უნდა არსებობდეს წარსულის განსაკუთრებული მდგომარეობა, რომელიც უნდა დაუმატო ბუნების ცნობილ კანონებს. ჩვენ ვაჩვენეთ, რომ არსებობს დროის ისარი, რომელიც არსებობს ნიუტონის თეორიის სტრუქტურიდან გამომდინარე და ის დაკავშირებული ამ u ფორმის მრუდთან. თუმცა, ეს მრუდი აღწერს მხოლოდ სისტემის ზომას. არსებობს კიდევ ერთი სიდიდე, რომელიც აღწერს თუ რამდენად კლასტერულადაა განაწილებული ნაწილაკები, ამ სიდიდეს კომპლექსურობას ვუწოდებთ. მაგალითად, თუ ცაში ვარსკვლავების განაწილებას დააკვირდები, ისინი არა ერთგვაროვნად, არამედ კლასტერულადაა განაწილებული, რის გამოც ძველმა კულტურებმა მათში თანავარსკვლავედები ამოიცნეს.

როდესაც ნიუტონისეული სისტემა ამ მინიმალურ ზომას აღწევს, ამ რეგიონის, იანუსის წერტილის ირგვლივ ნაწილაკები უფრო ერთგვაროვნადაა განაწილებული ვიდრე მის ორივე მხარეს. თუ რომელიმე მიმართულებით გადაადგილდები, იზრდება კლასტერების რაოდენობა და შესაბამისად კომპლექსურობა და წესრიგი. ეს კლასტერები, რაც უფრო შორდები იანუსის წერტილს, იქცევიან როგორც გალაქტიკები, რომლებიც ბრუნავენ ცენტრის გარშემო, ასევე ნაწილაკთა წყვილები, რომლებიც ერთმანეთის გარშემო ელიფსურ ორბიტებზე მოძრაობენ, როგორც ეს კეპლერმა აჩვენა, ამათ კეპლერის წყვილებს ვუწოდებთ. ამრიგად, როცა იანუსის წერტილში ხარ, ამ მინიმალურ ზომაში, ნაწილაკები მეტნაკლებად ერთგვაროვნად ნაწილდებიან, ფუტკრების დაჯგუფებასავით და ყველა მიმართულებით გადაადგილდებიან, მაგრამ როგორც კი შორდები ამ წერტილს, წარმოიქმნება საოცარი სტრუქტურები, რაც უწესრიგობის ზრდის საპირისპიროა და არაფრით ჰგავს ენტროპიის ზრდას. ეს იყო 2014 წელს ჩვენ მიერ გამოქვეყნებული სტატიის ძირითადი იდეა.

სპინოზას ჰქონდა "კონატუსის" კონცეფცია, რაც აღნიშნავს საგნების თვითგაუმჯობესების თანდაყოლილ უნარს. ბოლო დროა ეს კონცეფცია გააცოცხლა რამდენიმე ავტორმა ბიოლოგიასთთან მიმართებით. როგორ, ფიქრობთ, კომპლექსურობის ზრდის თქვენეული კონცეფცია ახლოსაა კონატუსთან? როგორ უნდა განვსაზღვროთ კომპლექსურობა მათემატიკურად?

ვფიქრობ, ნამდვილად არსებობს კავშირი ამ ორს შორის. მე არ ვარ სპინოზას ექსპერტი, მაგრამ ცნობილია, რომ ლაიბნიცმა ბევრი თავისი საკვანძო იდეა სპინოზასგან ისესხა. კერძოდ, ლაიბნიცი ყოველთვის საუბრობს სამყაროს სრულყოფილებისკენ სწრაფვაზე, რაც ჰგავს იმას, როგორც შენ აღწერ სპინოზას კონატუსს.

რაც შეეხება კომპლექსურობის მათემატიკურ განმარტებას. პირველ რიგში, კომპლექსურობა უნდა იყოს წმინდა რიცხვი და რაღაც, რაც დამოკიდებულია მხოლოდ ფორმაზე. სიმარტივისთვის, წარმოიდგინე, რომ გვაქვს ნაწილაკები სივრცეში და ყველა ნაწილაკს ერთნაირი მასა აქვს. ამრიგად, საქმე გვაქვს სივრცეში არსებულ წერტილებთან და მე მჭირდება რაღაც, რაც მეტყვის რამდენად კლასტერულად არიან ისინი განაწილებულები, რაც უნდა იყოს დამოკიდებული ზომაზე, ანუ მასშტაბის მიმართ ინვარიანტული უნდა იყოს. გაქვს ორი რიცხვი. ერთია მასებით გასაშუალოებული კვადრატული სიგრძის ფესვი, სადაც ნაწილაკების წყვილების კომბინაციას ამრავლებ მათ შორის მანძილის კვადრატზე, ჰყოფ მასათა ჯამზე და შემდეგ ამოიღებ ფესვს.

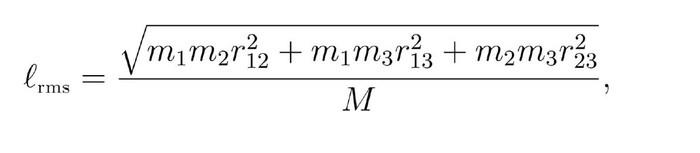
მეორე რიცხვია საშუალო ჰარმონიული სიგრძე, სადაც ამრავლებ ნაწილაკის მასებს და ჰყოფ მათ შორის მანძილზე და აჯამებ თითოეულს:

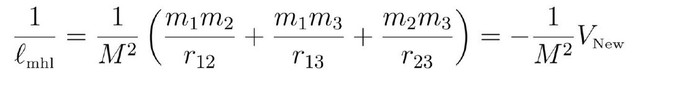
თუ მასებით გასაშუალოებული კვადრატული სიგრძის ფესვს გავყოფთ საშუალო ჰარმონიულ სიგრძეზე, მივიღებთ იმას, რასაც მე კომპლექსურობას ვუწოდებ:

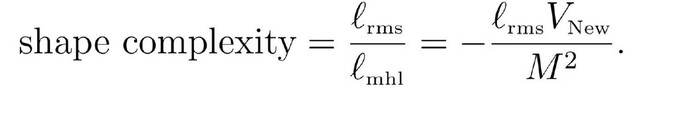
ვფიქრობ, უინტერესო ერთგვაროვნებიდან კომპლექსურობის და წესრიგის ზრდის ეს ტენდენცია, რაც სამყაროში გვაქვს, შექმნის თეორიაზე (creation), ან გნებავთ სპინოზას კონატუსის ან ლაიბნიცის სწრაფვის თეორიაზე მიუთითებს.

იტყოდით, რომ თქვენი ნაშრომები პარმენიდეანულია?

პარმენიდე ცნობილია მისი თეორიის გამო, რომ დრო და ცვალებადობა ილუზიაა. ამას საკმაოდ სერიოზულად მივუდექი ჩემ წინა ნაშრომში “დროის აღსასრული” და დღემდე საკმაოდ პარმენიდეანელი ვარ, მაგრამ უფრო ვიტყოდი რომ პლატონისტი ვარ მათემატიკასთან მიმართებაში. მაგალითად, მე ვფიქრობ, რომ არსებობს ყველა შესაძლო სამკუთხედის სივრცე - მათემატიკურ ფორმათა სამყაროში. ბევრ რამეში არ ვეთანხმები როჯერ პენროუზს, მაგრამ მათემატიკურ პლატონიზმში ჩვენი მოსაზრებები თანხვდება.