ბევრი ადამიანი ფიქრობს და მათ შორის, შესაძლოა, თქვენც მიიჩნევდეთ, რომ მათემატიკა ადამიანის გამოგონებაა. ამ ლოგიკით, შეგვიძლია იგი სასაუბრო ენასთანაც კი გავაიგოვოთ: მართალია, ის სამყაროში არსებულ რეალურ საგნებს აღწერს, თუმცა მათემატიკა არ არსებობს ჩვენი, მისით მოსარგებლეთა გონების გარეთ.

ასეა თუ ისე, ძველ საბერძნეთში პითაგორეიზმის მიმდევრები ამ საკითხს განსხვავებულად ხედავდნენ და სჯეროდათ, რომ რეალობა არსებითად მათემატიკურია.

2 ათასზე მეტი წლის შემდეგ ფილოსოფოსებმა და ფიზიკოსებმა გადაწყვიტეს, ამ აზრისათვის სერიოზულად შეეხედათ, ახალ ნაშრომში კი ვცდილობ დავამტკიცო, რომ მათემატიკა ბუნების არსებითი კომპონენტია, რომელიც ფიზიკურ სამყაროს სტრუქტურას ანიჭებს.

მეთაფლია ფუტკრები და ექვსკუთხედები

ალბათ, არაერთხელ შეგიმჩნევიათ, რომ ფუტკრები სკაში ექვსკუთხა ფიჭას წარმოქმნიან.

მათემატიკაში არსებულ "ფიჭურ ჰიპოთეზაზე" დაყრდნობით, ჰექსაგონები ანუ ექვსკუთხედები, სიბრტყის დასაფარად ყველაზე ეფექტური ფორმაა — თუ გსურს, ერთგვაროვანი ფორმისა და ზომის ფილებით ზედაპირი სრულად დაფარო და თან პერიმეტრის საერთო სიგრძე მინიმუმამდე შეინარჩუნო, ჰექსაგონები ამისათვის საუკეთესო ვარიანტია.

როგორც ჩარლს დარვინი ვარაუდობდა, ფუტკრები ევოლუციით ამ ფორმის გამოყენებამდე მივიდნენ, რადგან ასე თაფლისათვის ყველაზე დიდი უჯრები წარმოიქმნება, ფუტკრის ცვილის შესაქმნელად კი მინიმალური რაოდენობის ენერგია იხარჯება.

ფიჭური ჰიპოთეზა პირველად უძველეს დროში გაჟღერდა, თუმცა მისი დამტკიცება მხოლოდ 1999 წელს შეძლო მათემატიკოსმა თომას ჰეილსმა.

მგალობელი ჭრიჭინობელები და მარტივი რიცხვები

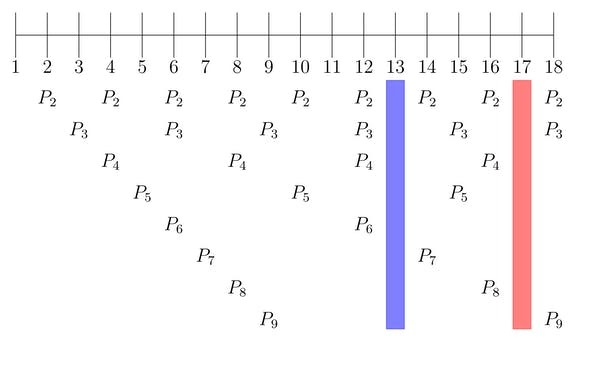
შეგვიძლია, ამას გარდა სხვა მაგალითიც მოვიყვანოთ. ჩრდილოამერიკულ პერიოდულ ჭრიჭინობელათა ორი ქვესახეობა არსებობს, რომელიც სიცოცხლის დიდ ნაწილს მიწისქვეშ ატარებს. ქვესახეობის მიხედვით, ყოველი 13 ან 17 წლის შემდეგ ჭრიჭინობელები მიწიდან დიდ გუნდებად ამოდიან და ზემოთ, დაახლოებით, ორი კვირის განმავლობაში რჩებიან.

შესაძლოა, გაგიჩნდეთ კითხვა: რაღა მაინცდამაინც 13 ან 17 და არა 12 და 14 ანდა — 16 და 18?

13 და 17 მარტივი რიცხვებია, ანუ ორივე მათგანი მხოლოდ ერთსა და საკუთარ თავზე იყოფა, ერთ-ერთი ახსნა კი სწორედ ამ ფაქტს ეყრდნობა.

წარმოიდგინეთ, რომ მგალობელ ჭრიჭინობელებს არაერთი მტერი ჰყავთ, რომლებიც სიცოცხლეს ძირითადად მიწაში ატარებენ. აქედან გამომდინარე, ჭრიჭინობელები მიწიდან მაშინ უნდა ამოვიდნენ, როდესაც მტაცებელი მიწისქვეშ იქნება.

ვივარაუდოთ, რომ მტაცებელთა სასიცოცხლო ციკლები 2, 3, 4, 5, 6, 7, 8 და 9 წლებისაგან შედგება. შესაბამისად, რა იქნება საუკეთესო გზა ყოველი მათგანისათვის თავის ასარიდებლად?

მაშ, 13 და 12-წლიანი სასიცოცხლო ციკლები შევადაროთ ერთმანეთს: თუ მიწიდან 12 წლიანი სასიცოცხლო ციკლის მქონე ჭრიჭინობელა ამოვა, 2, 3 და 4-წლიანი ციკლის მქონე მტაცებლებიც ზემოთ იქნებიან, რადგან 12 უნაშთოდ იყოფა 2-ზეც, 3-ზეც და 4-ზეც.

ამის საპირისპიროდ კი, თუ მიწიდან 13-წლიანი სასიცოცხლო ციკლის მქონე ჭრიჭინობელა ამოვა, ზემოთ არც ერთი მტაცებელი არ დახვდება, ვინაიდან 13 უნაშთოდ ზემოთჩამოთვლილ არცერთ ციფრზე არ იყოფა. სწორედ იგივე პრინციპი მოქმედებს 17-ის შემთხვევაშიც.

როგორც ჩანს, ჭრიჭინობელები იმგვარად განვითარდნენ, რომ ახერხებენ და რიცხვებთან დაკავშირებულ ძირითად ფაქტებს თვითგადარჩენის პროცესში აქტიურად იყენებენ.

შექმნა თუ აღმოჩენა?

თუ მოვძებნით, არც სხვა მაგალითების პოვნა გაგვიჭირდება — მათემატიკა ყველგანაა, საპნის აფსკებში იქნება ეს, ძრავების მექანიზმთა დიზაინში თუ სატურნის რგოლებს შორის არსებულ ნაპრალთა ზომებსა და განლაგებაში.

იმის გავითვალისწინებთ, თუ რამდენ რამეს ხსნის მათემატიკა ჩვენ გარშემო, ნაკლებად სავარაუდოა, რომ იგი ჩვენი შექმნილი რამაა, ამის ალტერნატივა კი უბრალოდ მათემატიკურ ფაქტთა აღმოჩენაა: ფაქტები აღმოვაჩინეთ არა მხოლოდ ადამიანებმა, არამედ მწერებმა, საპნის ბუშტებმა, წვის ძრავებმა და პლანეტებმაც კი.

რას ფიქრობდა პლატონი?

თუ რაღაცის აღმოჩენის პროცესში ვართ, ისიც ხომ უნდა ვიცოდეთ, რა არის იგი? ძველ საბერძნეთში მცხოვრებ ფილოსოფოს პლატონს ამაზე პასუხი ჰქონდა და ფიქრობდა, რომ მათემატიკა რეალურად არსებულ ობიექტებს აღწერს.

პლატონისათვის საგნებს შორის რიცხვები და გეომეტრიული ფორმებიც გახლდათ, დღესდღეობით კი შეგვიძლია, ამას მეტად ჩახლართული მათემატიკური ობიექტებიც დავამატოთ: ჯგუფები, კატეგორიები, ფუნქციები, ველები და რგოლები.

პლატონი ასევე ამტკიცებდა, რომ მათემატიკური ობიექტები სივრცისა და დროის მიღმაც არსებობს, მისეული ახსნა კი იმის წარმოჩენასაც მოიცავს, თუ როგორაა სამყაროში ერთი რამ დამოკიდებული მეორეზე. თუ მათემატიკური ობიექტები ჩვენი რეალური სამყაროს მიღმაც არსებობს, სავარაუდოდ, ისინი არაფერ ფიზიკურს არ უკავშირდება.

ცოტა რამ პითაგორეიზმის შესახებ

პითაგორეიზმის ძველი მიმდევრები პლატონს ეთანხმებოდნენ და თვლიდნენ, რომ მათემატიკა საგანთა სამყაროს აღწერს, თუმცა, მისგან განსხვავებით, არ მიიჩნევდნენ, რომ მათემატიკური ობიექტები სივრცისა და დროის მიღმაც არსებობს. ისინი ფიქრობდნენ, რომ ფიზიკური რეალობა ისევეა მათემატიკური ობიექტებისაგან შექმნილი, როგორც ნივთიერებები — ატომებისგან.

თუ რეალობა მართლაც მათემატიკური ობიექტებისგანაა შექმნილი, მარტივი დასანახია, თუ როგორ შეიძლება მათემატიკამ ჩვენი სამყაროს ახსნაში შეიძინოს როლი.

უკანასკნელი ათწლეულის განმავლობაში ორმა ბუნებისმეტყველმა — კოსმოლოგმა მაქს თეგმარკმა და ფიზიკოს-ფილოსოფოსმა ჯეინ მაკდონელმა — პითაგორასეულ პოზიციას საკმაოდ მნიშვნელოვანი არგუმენტი მოუძებნა.

თეგმარკის მტკიცებით, რეალობა ერთი უზარმაზარი მათემატიკური ობიექტია. თუ ეს უცნაურად ჟღერს, გაიხსენეთ იდეა, რომ რეალობა სიმულაციაა. სიმულაცია კომპიუტერული პროგრამაა, რომელიც ასე თუ ისე მათემატიკურ ობიექტს წარმოადგენს.

ამის პარალელურად, მაკდონელის ხედვა მეტად რადიკალურია: მისი აზრით, რეალობა მათემატიკური ობიექტებისა და აზრებისაგან შედგება, ხოლო მათემატიკა კი გზაა, რომლითაც ცნობიერი სამყარო საკუთარ თავს შეიცნობს.

აღსანიშნავია ისიც, რომ მე ამისაგან განსხვავებული მოსაზრება მაქვს: სამყაროს ორი ნაწილი აქვს, მათემატიკა და მატერია. მათემატიკა მატერიას აძლევს ფორმას, მატერია კი მათემატიკას ანიჭებს სუბსტანციას. მათემატიკური ობიექტები ფიზიკური სამყაროსათვის სტრუქტურულ კარკასს უზრუნველყოფს.

მათემატიკის მომავალი

გონივრულია, რომ პითაგორეიზმის ფიზიკაში ხელმეორედ აღმოჩენის მომსწრენი ვხდებით. გასულ საუკუნეში ფიზიკა თანდათანობით უფრო მათემატიკური გახდა და ფიზიკური სამყაროს ამოსახსნელად გამოკვლევის ერთი შეხედვით აბსტრაქტული სფეროებისაკენ წავიდა, როგორიცაა ჯგუფთა თეორია და დიფერენციალური გეომეტრია.

რაც მეტად იშლება ზღვარი ფიზიკასა და მათემატიკას შორის, მით უფრო რთული სათქმელი ხდება ისიც, თუ სამყაროს რომელი ნაწილებია ფიზიკური და რომელი — მათემატიკური. საკმაოდ უცნაურია ის ფაქტიც, რომ პითაგორეიზმი ფილოსოფოსებმა ამდენი ხნის განმავლობაში მიივიწყეს, მე კი ვფიქრობ, რომ ეს ყველაფერი შეიცვლება. პითეგორასეული რევოლუციის დრო მოვიდა, რაც რეალობის ჩვენეული გაგების რადიკალურ ცვლილებას მოასწავებს.

თუ სტატიაში განხილული თემა და ზოგადად: მეცნიერებისა და ტექნოლოგიების სფერო შენთვის საინტერესოა, შემოგვიერთდი ჯგუფში – შემდეგი ჯგუფი.